分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
データセットが与えられたとき、主成分分析や t-SNE によりデータセットの可視化をすることがあります。

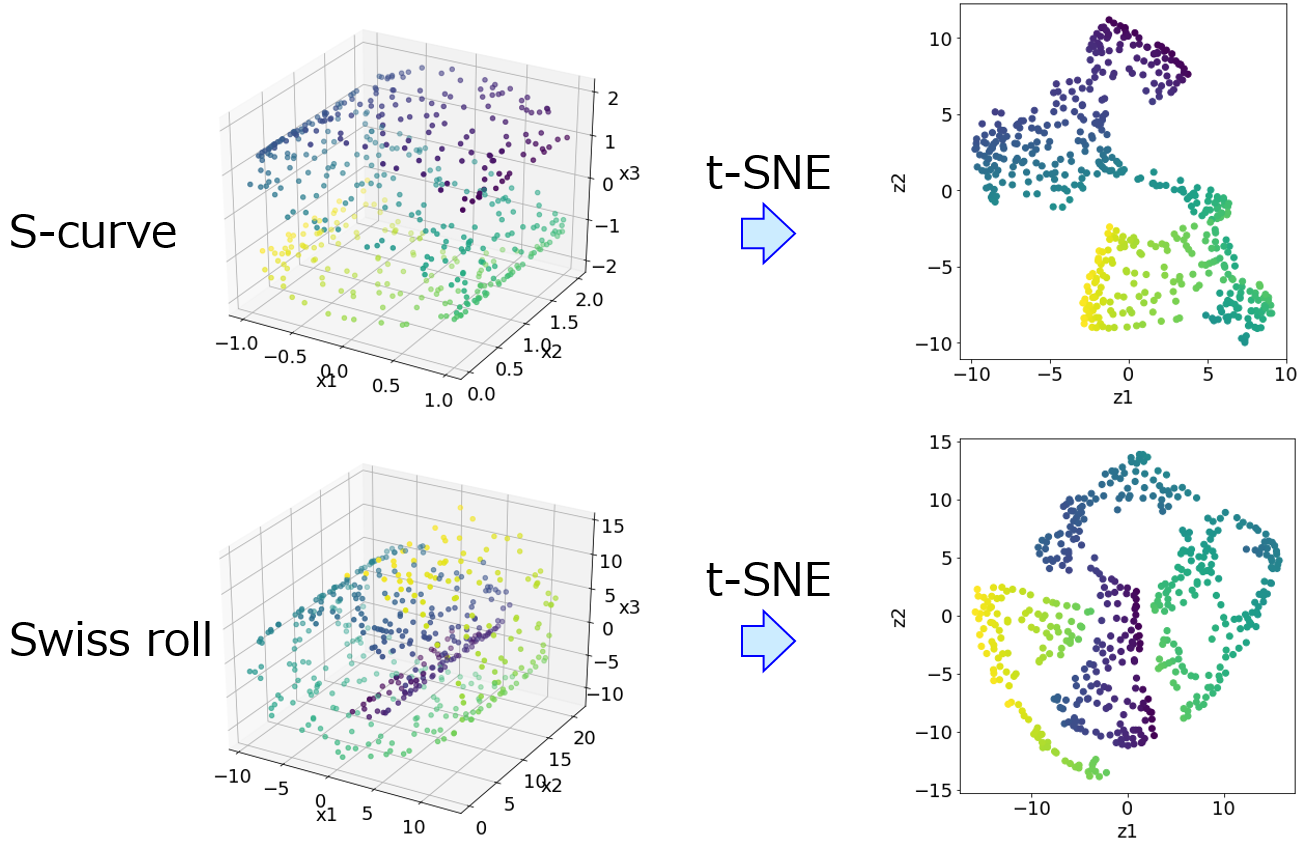
x を例えば2つの潜在変数に (2次元に) 低次元化して、その潜在変数の空間におけるサンプルの分布を散布図で確認します。これにより、各サンプルの位置関係を視覚的に確認できます。
一方で、実験計画法においては、同様のデータセットの可視化をすることは難しいです。そもそも実験計画法では、まだ実験データがない中で、初期実験をするときに、実験条件の最初の候補として、なるべく類似していない、ばらついた候補を作成します。x 間の相関係数でいえば、なるべく 0 に近いように候補サンプルを選択することに相当します。
そもそも x の低次元化は、x 間に情報の重複があるデータセットにおいて、x の情報を圧縮して より少ない数の潜在変数で表現することであり、x 間に情報の重複があることが前提になります。実験計画法においては x 間の情報の重複がないようにサンプルを選択しているため、低次元化がうまくいきません。主成分分析でいえば、第一、第二主成分の累積率がとても小さくなります。
もちろん例外もあります。実験計画法におけるサンプルに化合物が含まれ、x に分子記述子があるとき、x の間には潜在的に相関関係があるものが存在しますので、低次元化で情報を圧縮した上で二次元平面上に適切に可視化することを期待できます。
多くの場合において、実験計画法におけるデータの可視化は難しいため、それ以外の方法でサンプル間の関係を見極める必要があります。その1つの方法がベイズ最適化です。

y の予測値だけでなく その分散を考慮することで、y の目標が遠いときには、y の予測値が良好な x の候補よりはむしろ、予測値の分散が大きいサンプルを選択します。ある x のサンプルにおける予測値の分散は、トレーニングデータの各サンプルとの間の距離に基づいて計算されますので、データセットを可視化して確認することはできませんが、トレーニングデータから遠いサンプルか近いサンプルかは考慮した上で、次の x の候補を選択できます。ベイズ最適化ではサンプル間の関係が自動的に考慮されますが、もちろんモデルの適用範囲を用いて明示的にサンプル間の距離関係を計算することもできます。

ちなみに直接的逆解析法では、確率密度分布の形でサンプル間の関係が考慮されます。
実験計画法においては、データの可視化が難しい一方で、サンプル間の関係を考慮しなくてよいわけではありませんので、適切にサンプル間の関係を確認して解析するようにしましょう。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


