[デモのプログラムあり] ガウス過程回帰(Gaussian Process Regression, GPR)におけるカーネル関数を11個の中から最適化する (scikit-learn)

こちらのガウス過程による回帰 (Gaussian Process Regression, GPR)

ガウス過程回帰(Gaussian Process Regression, GPR)～予測値だけでなく予測値のばらつきも計算できる！～

ガウス過程による回帰(Gaussian Process Regression, GPR)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、GPRで何ができるか、GPRをどのように計算するかが説明されていま...

において、カーネル関数をどうするか、というお話です。

そもそも GPR のカーネル関数はサポートベクター回帰 (Support Vector Regression, SVR) のそれとは異なります。

サポートベクター回帰(Support Vector Regression, SVR)～サンプル数10000以下ならこれを使うべし！～

サポートベクター回帰(Support Vector Regression, SVR)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、SVRで何ができるか、SVRの特徴、どのように計算するかが説明されてい...

いつも使っているガウシアンカーネルもしくは RBF (Radial Basis Function) カーネルを、そのまま使えないのですね (モデリングはできますが、推定精度が下がってしまいます)。その理由は GPR モデルの導出過程にあります。GPR のカーネルは目的変数 y の (サンプル間の) 分散もしくは共分散を表し、そこには回帰係数の分散の項や、y の測定誤差の分散の項があるため、ガウシアンカーネルのような SVR で用いるようなカーネル関数に、定数項を掛けたり足したりしないといけないのです。詳しくはこちらをご覧ください (資料を更新しました！)。

ガウス過程回帰(Gaussian Process Regression, GPR)～予測値だけでなく予測値のばらつきも計算できる！～

あと、GPR ではカーネル関数におけるパラメータの数を多くする傾向があります。SVR では、カーネル関数におけるパラメータ (ガウシアンカーネルの γ) をクロスバリデーションで最適化する必要があるため、パラメータの数が多いことは、最適化に多くの時間がかかることであり望ましくありませんでした。GPR では、その必要はなく、モデリングのときに最尤推定法でパラメータの値を決められます。なので、パラメータの数を多くしても計算時間的にそれほど問題ではないわけです。

もちろん、パラメータの数が多いとオーバーフィッティングの危険が増えますので、

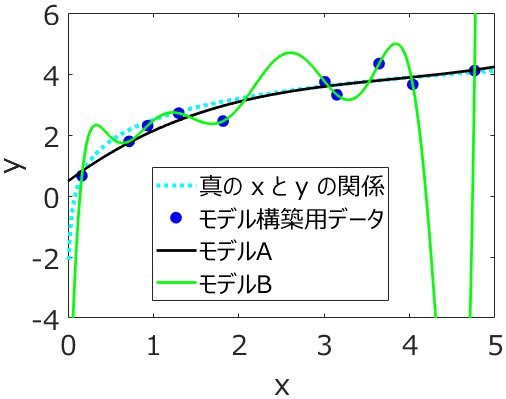
人工知能・機械学習のときには過学習 (オーバーフィッティング) に気をつけよう！～過学習とその対処法～

応化先生と生田さんが過学習 (オーバーフィッティング) について話しています。応化：今日は過学習についてです。生田：過学習？学習し過ぎるってこと？応化：その通りです。生田：だったら悪いことじゃなさそうに聞こえるけど・・・。学習をたくさんする...

多くすればするほどよいわけではありません。なので、パラメータの数がいい塩梅の以下のカーネルをよく使用しています。

これまでのサンプルプログラムでもこちらを使用していました (scikit-learn における ConstantKernel() * RBF() + WhiteKernel() です)。オススメです。

ただ、データセットによっては、より適したカーネル関数があることも考えられます。そんな場合は、こちらの「GPRで使われるカーネル関数の例」

ガウス過程回帰(Gaussian Process Regression, GPR)～予測値だけでなく予測値のばらつきも計算できる！～

の中から最適化しています。scikit-learn では以下のとおりです。

ConstantKernel() * DotProduct() + WhiteKernel()
ConstantKernel() * RBF() + WhiteKernel()
ConstantKernel() * RBF() + WhiteKernel() + ConstantKernel() * DotProduct()
ConstantKernel() * RBF(np.ones(n_features)) + WhiteKernel()
ConstantKernel() * RBF(np.ones(n_features)) + WhiteKernel() + ConstantKernel() * DotProduct()
ConstantKernel() * Matern(nu=1.5) + WhiteKernel()
ConstantKernel() * Matern(nu=1.5) + WhiteKernel() + ConstantKernel() * DotProduct()
ConstantKernel() * Matern(nu=0.5) + WhiteKernel()
ConstantKernel() * Matern(nu=0.5) + WhiteKernel() + ConstantKernel() * DotProduct()
ConstantKernel() * Matern(nu=2.5) + WhiteKernel()
ConstantKernel() * Matern(nu=2.5) + WhiteKernel() + ConstantKernel() * DotProduct()

n_features には説明変数 X の変数の数が入ります。

最適化する方法は、大きく分けて 2 つあります。

それは、それぞれのカーネル関数で

クロスバリデーションを行い
モデル構築し、テストデータを予測して、

たとえば r² が最も大きいカーネル関数を使用する方法です。

1. のクロスバリデーションで最適化する方法では、テストデータを用いていませんので、テストデータにオーバーフィットする心配はありませんが、クロスバリデーションでモデル構築と予測を繰り返しますので、時間がかかります。時間に余裕があるときはこちらがよいでしょう。

2. のテストデータを用いる方法では、カーネル関数ごとにモデル構築は 1 回で済みますので、1. の方法と比べて時間がかかりません。カーネル関数ごとに別の手法と考えて、(PLS や SVR などの) 他の手法と並行して比較する感じです。しかし、テストデータにオーバーフィットするカーネル関数が選ばれる危険があります。

それぞれ、カーネル関数の最適化のデモンストレーションの Python プログラムを準備しました。こちら https://github.com/hkaneko1985/dcekit にある、demo_gp_kernel_design_cv.py がクロスバリデーションで最適化するデモ、demo_gp_kernel_design_test.py がテストデータで最適化するデモです。ぜひご利用ください。

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。