回帰分析やクラス分類の話です。データセットがあるとき、まずモデル構築用データ (トレーニングデータ) とモデル検証用データ (テストデータ) に分けます。次にトレーニングデータで回帰モデル・クラス分類モデルを構築します。そして、モデル構築に用いていない新しいデータであるテストデータで、構築されたモデルがどのくらいの精度をもつか検証を行います。

テストデータにおいて説明変数 X の値から目的変数 y の値を推定したとき、全体的にトレーニングデータにおける推定誤差と同じくらいの誤差であれば happy、というわけです。しかしながら、いつもそうとは限りません。
トレーニングデータの y の値は精度よく (誤差は小さく) 推定できたのに、テストデータにおける y の値の推定誤差が大きくなってしまった!ってことも起こります。あまりうれしくない話ですね。こんなとき、モデルがトレーニングデータにオーバーフィット (過学習) したのかなぁ、とか、テストデータがモデルの適用範囲の外なのかなぁ、とか、テストデータに外れ値があるのかなぁ、とか議論するわけです。
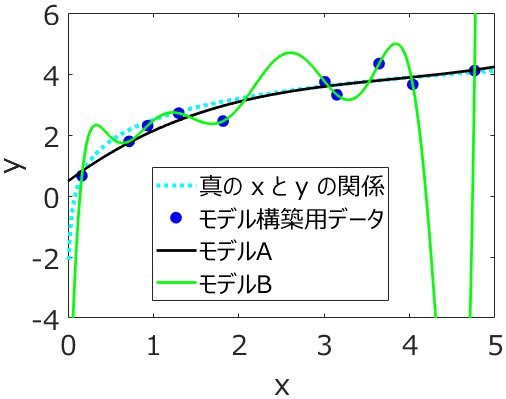

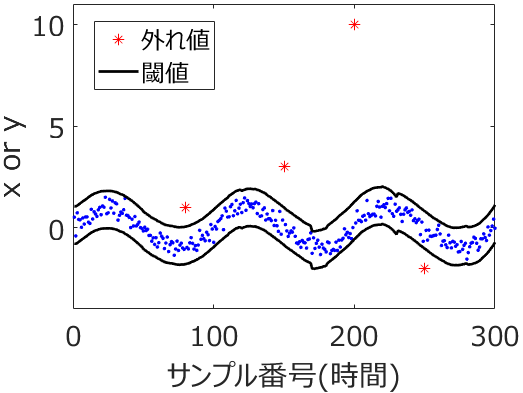
もちろん、こういった議論は大事です。ただ、テストデータにおける推定精度が低いときにも、うれしいと思えることはあります。
それは
X と y の間の新しい関係を発見できたかも!?
ということです。トレーニングデータにおける X と y との間の関係を表現したモデルでは、テストデータにおける X と y との間の関係を表現できなかったということは、トレーニングデータにおける関係とは異なる関係がテストデータにはあるはずです。
そもそもの回帰分析・クラス分類の目的は、今あるすべてのデータセットを用いて X と y との間のモデルを構築することで、y の値がわからないデータにおいて、X の値のみから y の値を推定することです。トレーニグデータで構築したモデルと、最終的に用いるモデルとは異なります。最終的に用いるモデルは、トレーニグデータもテストデータも含むすべてのデータを用いて構築されたモデルなわけです。テストデータの X と y との間の関係を、最終的に用いるモデルに取り込めることで、より多様な X と y との間の関係をモデルで考慮できるようになります。モデルの適用範囲も広がるでしょう。
100点満点の試験で50点を取ってしまっても、復習して次に100点を取れれば OK !! といった感じでしょうか。むしろ試験を通して成長できていますね。
もちろん、トレーニグデータでは良好なモデルが構築できたことが前提の話ですし、最終的なモデルを構築するときも、y-randomization やモデルの適用範囲を検討する必要はあります。


ただ、テストデータにおけるモデルの精度が低いとき、ただ落ち込むだけでなく、このようなポジティブな側面もあることを考えていただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


