目的変数 Y と説明変数 X との間で回帰モデル Y = f(X) を構築するとき、基本的にモデルの適用範囲 (Applicability Domain, AD) を設定する必要があります。AD の詳細はこちらをご覧ください。


回帰分析手法であるサポートベクター回帰 (Support Vector Regression, SVR) を用いるとき、

X と Y の間の非線形性を考慮するため、カーネル関数を用いることが多いです。カーネル関数の中で、特によく用いられるのはガウシアンカーネルと思います。
あるサンプル x(i) と別のサンプル x(j) の間では、ガウシアンカーネルは以下のように計算されます。
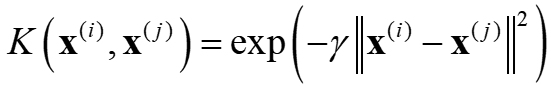
γ はハイパーパラメータであり、こちらのように高速に決めることもできます。

ガウシアンカーネルを用いたとき、SVR モデルは以下のようになります。
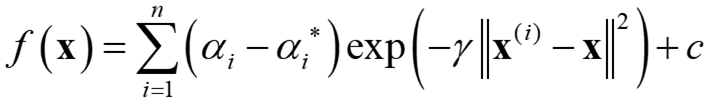
n はサンプル数であり、n = 3 のとき (非常に小さいですが、説明のしやすさのため 3 にしています) 以下のような式で表されます。
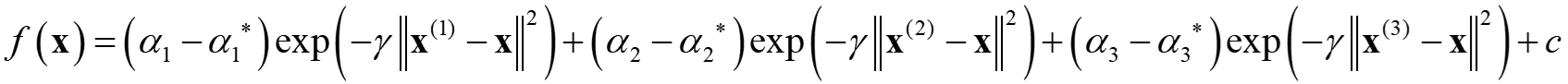
新しいサンプル x における Y の値を予測するとき、x とトレーニングデータの各サンプルとの間のユークリッド距離に基づく類似度 (ガウシアンカーネルの値) と、(αi − αi*) との積を足し合わせ、最後に定数項 c を足したもので Y の予測値が与えられることがわかります。さらにいえば、ε チューブ内のサンプルは、αi = 0, αi* = 0 となり Y の予測値には寄与しません。
いま、Y の値を予測したいサンプル x が、トレーニングデータの各サンプルから非常に遠いときを考えます。x とトレーニングデータの各サンプル間の距離が非常に大きいということです。このとき、ガウシアンカーネルの値はほぼ 0 になります。そのため、(αi − αi*) × (ガウシアンカーネルの値) も 0 になりますので、Y の予測値は定数項 c になります。SVR モデルでは、Y の値を予測したいサンプルがトレーニングデータの各サンプルから遠いとき、予測値が一定値になるということです。皆さんの中にも、このような経験をされたことがあるかもしれません。予測値が一定の値になったとき、その値は c と考えられます。
上の式より、SVR モデルではトレーニングデータにおける代表サンプル (ε チューブ上および ε チューブ外のサンプル) との距離に基づきますので、サンプル間の距離で AD を決めることと同じ、といえるかもしれません。サンプル x とトレーニングデータの各サンプル間の距離が非常に大きい、すなわち AD 外のとき、Y の予測値が c 付近になります。しかし、予測値が c 付近にならなかったからといって AD 内といえるわけではありませんので、注意してください。AD 内を判定するときは、適切に AD を設定したほうがよいです。
線形の回帰モデルでは、Y の値を予測したいサンプルがトレーニングデータのサンプルから遠いほど、予測値が大きくなったり、逆に小さくなったりする可能性がありますが、ガウシアンカーネルを用いた SVR では、そのようなことはなく、トレーニングデータのサンプルから遠いときは予測値が c になり、AD 外、つまり予測は難しいということがわかります。しかし、サンプルがどれくらい離れているとき、どの程度の予測精度で予測できるかまではわかりません。それを検討するためには、適切に AD を設定する必要があります。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。