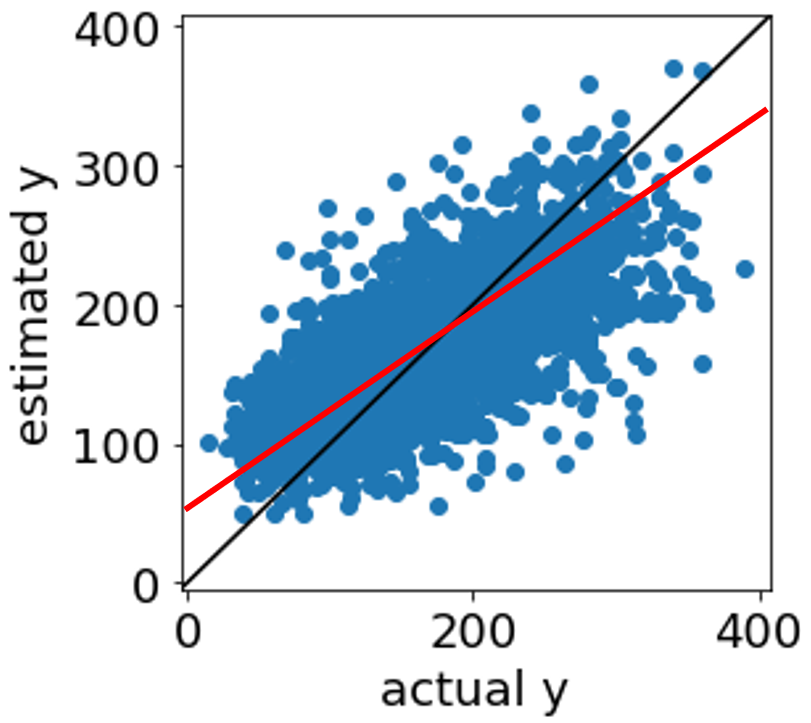
データセットを用いて、目的変数 Y と説明変数 X との間で回帰モデル Y = f(X) を構築し、そのモデルに X の値を入力することで Y の値を予測することがあります。その予測結果を、下の図のような Y の実測値 vs. 予測値のプロットを見ることで確認します。
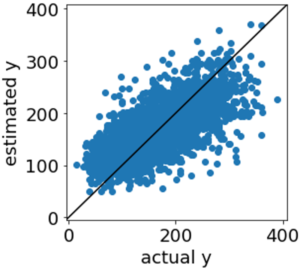
プロットにおいて、サンプルが対角線付近に均等に固まって分布しているほど、よい予測結果といえるのですが、上のようにサンプルが横に (対角線より小さい角度の方向に) 分布してしまうことがあります。いわゆるサンプルが 「寝る」 状態です。これは、Y の値が大きいサンプルが小さく予測され、Y の値の小さいサンプルが大きく予測されてしまうことを意味します。そのため、分子設計や材料設計を行うとき問題になります。つまり、Y の大きい分子や材料、Y の小さい分子や材料を目指そうとすることが難しくなります。プロットが寝ないように、いろいろと工夫されている方もいらっしゃると思います。下図の赤線くらいが対角線になるとうれしいですね。

プロットが寝る原因として、基本的に Y を説明するための情報が X に不足していることや、もしくは X に情報はありますが不要な情報に埋もれてしまい X から重要な情報を抽出できていないとことが考えられます。
ただ、線形モデルを構築するときは、プロットが寝ることはある程度仕方ない、ともいえます。この理由として、決定係数 r2 が、実測値 vs. 予測値プロットの分布の角度に関係していることが挙げられます。順を追って説明します。
一般的には、決定係数 r2 と、相関係数 r を2乗したもの (r)2 とは異なります。しかし、特に最小二乗法による線形回帰分析を行ったときのトレーニングデータにおいては、r2 = (r)2 となります。つまり決定係数の大きさと相関係数の大きさとが一致するわけです。単回帰分析におけるこの証明を念のためこちらに載せておきます。
そして相関係数 r は、特に各変数の平均値が 0 のときに、2 つの変数 (ベクトル) の角度を意味します。角度を θ としたとき、r = cos(θ) です。r = 1、つまり実測値と予測値とが一致するときのみ、cosθ = 1 より θ = 0° となり、対角線の方向に分布することになります。すなわち、r < 1 のとき、θ は 0° になることはなく、必ず対角線の方向から角度がズレてしまいます。r が 1、すなわち (線形回帰分析において) r2 = 1 のとき、プロットが寝るということです。
線形回帰分析には、このような性質があることは押さえておいた方がよいと思います。対角線分布のど真ん中を通らせたいときには、非線形の回帰分析手法を検討するのが一つの手です。ただし、非線形回帰分析手法を使うと必ずプロットが寝なくなるわけではありませんので注意しましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。