金子研の論文が Journal of Chemometrics に掲載されましたので、ご紹介します。タイトルは
Support vector regression that takes into consideration the importance of explanatory variables
です。
説明変数 X と目的変数 Y との間で回帰モデル Y = f(X) を構築するため、サポートベクター回帰 (Support Vector Regression, SVR) を使用することがあります。


モデル構築のときに X と Y の間の非線形性を考慮するために、最もよく使用されるカーネル関数はガウシアンカーネル (もしくは Radial Basis Function, RBF) カーネルです。ガウシアンカーネルを用いることで、良好なモデルを構築できることも多いですが、ガウシアンカーネルは、基本的にサンプル間のユークリッド距離に基づくカーネル関数であり、X はすべて同じように扱われます。X の中に重要な特徴量や重要でない特徴量が混在していても、それらの違いを表現できず、すべて同等に考慮されます。
事前に特徴量選択 (変数選択) をすることで、重要な特徴量のみ X として使用する、という戦略も考えられますが、特徴量の重要性にはグラデーションがあると考えられ、非常に重要な特徴量からほとんど重要でない特徴量まで連続的です。このような状況で、何かの閾値のようなものにより 「これらの特徴量は全く重要でない」、と切り捨ててしまうことには危険が伴います。
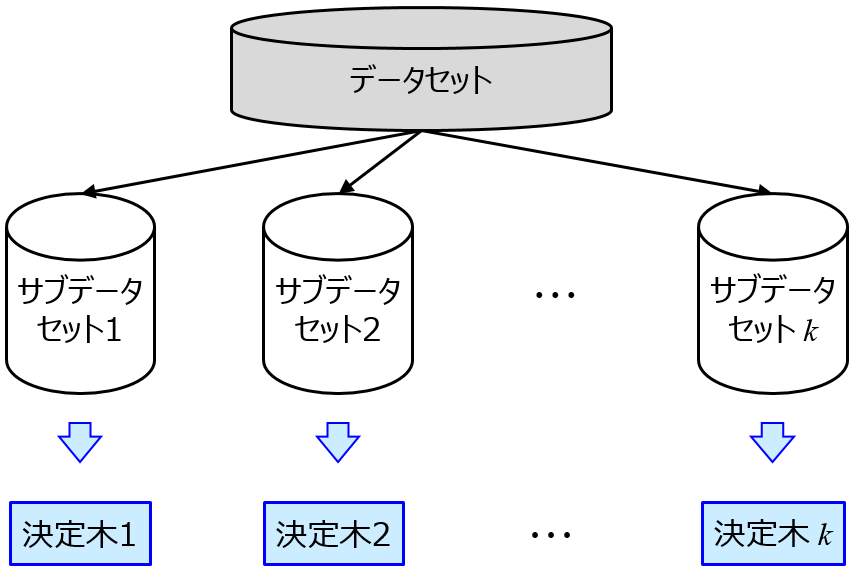
そこで、0 or 1 の特徴量選択ではなく、(0 から 1 の間のグラデーションである) 特徴量の重要度で重みを付けたカーネル関数を提案しました。具体的にはランダムフォレスト (Random Forests, RF) により、X と Y の間の非線形性を考慮した特徴量の重要度を計算します。
その重要度で重みをつけてから、カーネル関数におけるユークリッド距離を計算します。これにより重要な特徴量ほどモデルに対する寄与を大きくすることができます。言い換えると、RF は内挿に強い一方で外挿に弱く、
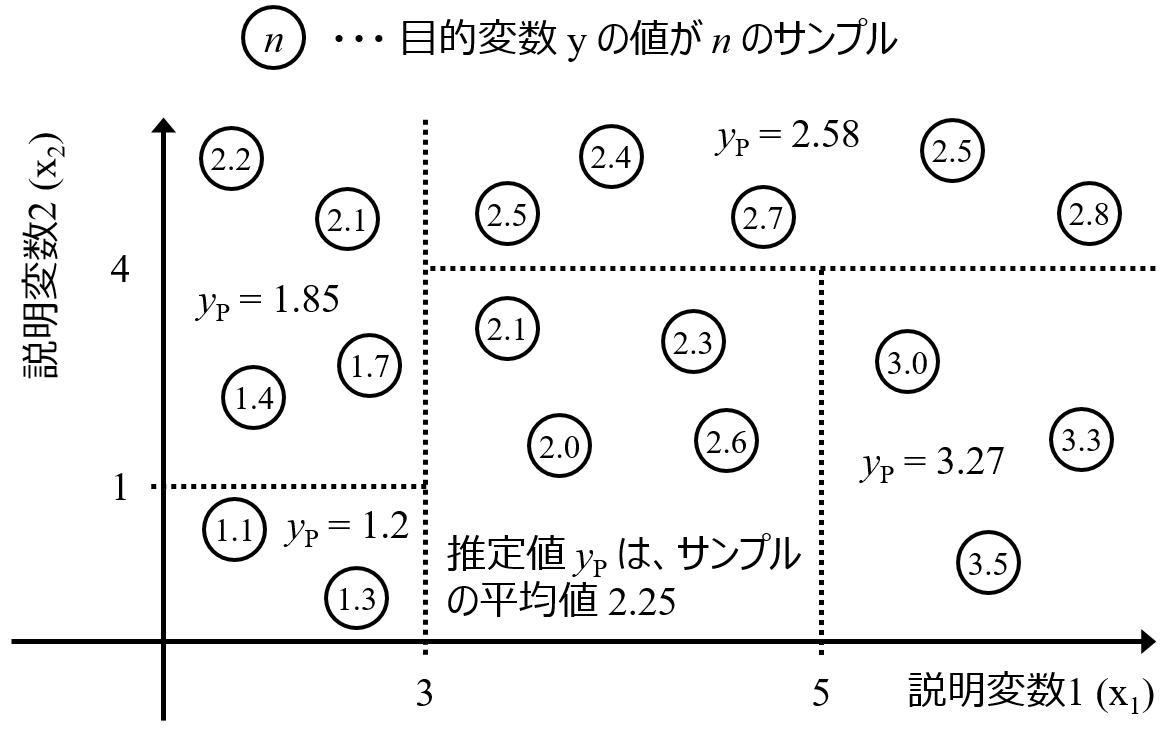
SVR は外挿に強いため、RF で (内挿の) 特徴量の重要度を計算し、それを SVR で外挿に展開する戦略です。
スペクトルデータの回帰分析や、QSPR, QSAR のデータ解析により提案手法の有効性を検証しています。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


