回帰モデルを直接的に逆解析ができる、すなわち説明変数 X から目的変数 Y (Y が複数でもOK!) を直接的に推定できる手法である Gaussian Mixture Regression (GMR) や Generative Topographic Mapping Regression (GTMR) について、論文を出したり、講演会でお話ししたりしています。
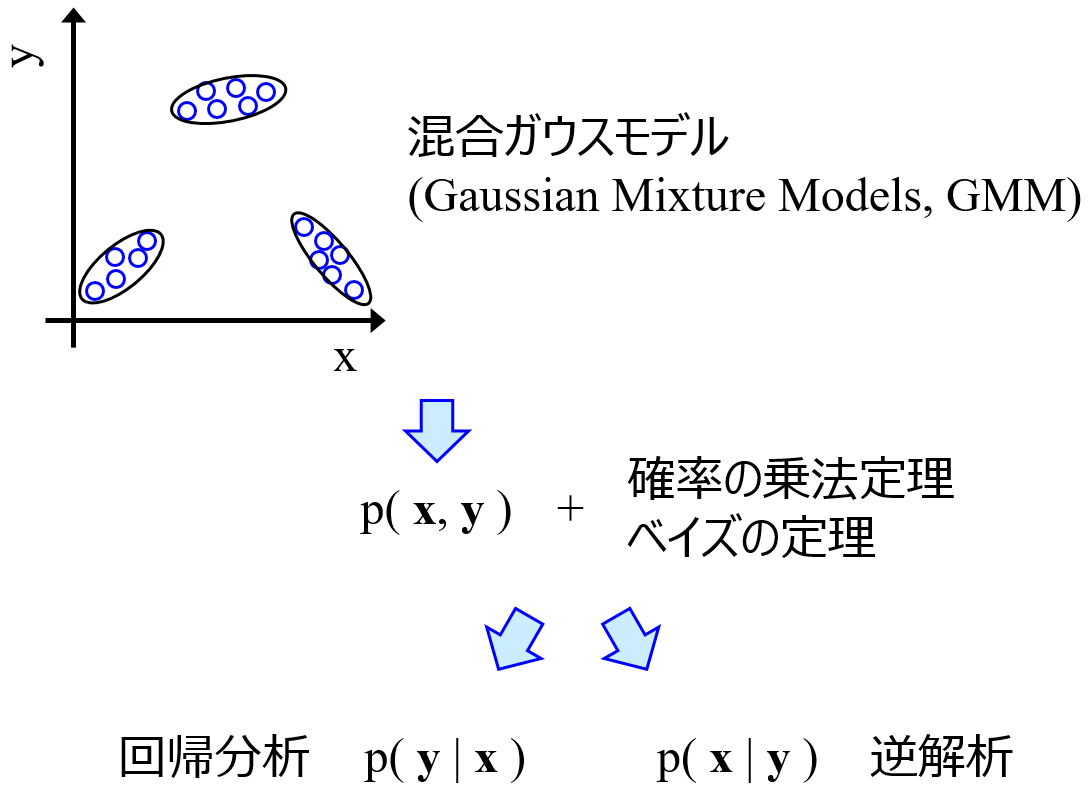

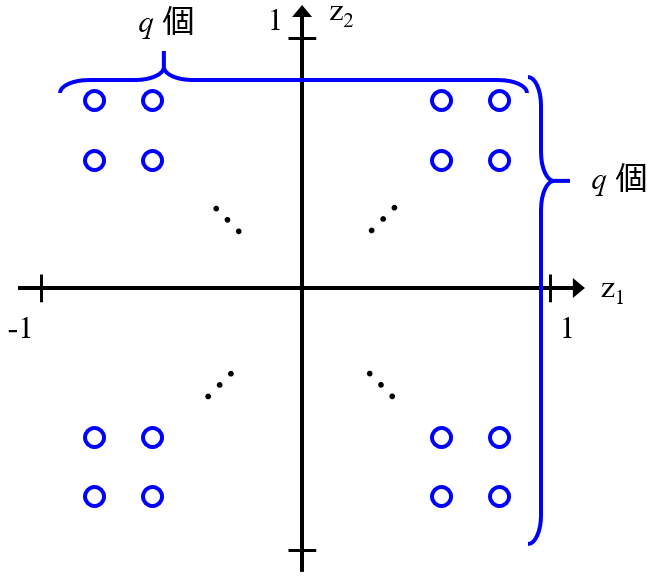
その結果、講演会での質問、メール、オンラインサロンなどで問い合わせをいただくことが多くなりました。
ちなみにオンラインサロンの会員数が 400 名を超えました!(会員数 401 名、2020年12月27日 現在) こちらも、どうもありがとうございます。引き続きよろしくお願いいたします。
ここでは、どうして一般的な擬似的なモデルの逆解析やベイズ最適化と比べて、直接的逆解析をする GMR や GTMR がうまくいくのか、整理しておきます。ただ、完全に解明されたわけではありませんので、現段階での仮説になります。
いわゆる一般的な擬似的な逆解析で行われていることは、X の仮想的なサンプルを乱数などで大量に生成して、それらをすべて予測して予測結果の中から良好なものを選ぶ、ということです。Y の推定値で選ぶこともあれば、ベイズ最適化のように推定値だけでなく推定値の分散も考慮して獲得算数の値に変換してから選ぶこともあります。遺伝的アルゴリズムなどの最適化アルゴリズムのように、Y の推定値が大きく (小さく) なるように、もしくは獲得関数の値が大きくなるように、X の値を最適化することもできます。
特にベイズ最適化では、外挿領域が探索されやすい、すなわち外挿領域における評価値 (獲得関数の値) が大きくなる傾向があります。ただ、外挿領域はかなり広いです。X の数が大きく (次元が高く) なるほど、指数関数的にデータ領域が増えていきますので、結果的に外挿領域も膨大になります。その膨大な外挿領域において、獲得関数の値が高いところを乱数で探索するため (もちろん最適化アルゴリズムで探索した場合でも)、探索ごとにある特定の場所の領域から仮想サンプルが得られるのではなく、探索ごとに異なる領域における仮想サンプルが得られることが多くなります。探索した後に実験して、また探索して実験して、を繰り返しますが、探索するごとにまったく別の領域からサンプルが得られることになり、結果的に探索ごとのサンプルの値がバラバラになることが多いです。疎なデータセットが得られることになります。もちろんこのような探索で上手くいくケースもあると思いますが、ある程度探索の方向性をもって、その方向にどんどん探索を繰り返したいケースもあるはずです。ただ、擬似的な逆解析では、そのような継続した外挿の探索というのは難しいです。
GMR や GTMR では、確率密度分布でモデルが表現され、Y の値を入力することでそれを達成する X の確率の高い値が推定されることから、膨大な外挿領域があるとはいえ、より確率の高いところという条件で、次の探索が行われます。そのため、これまでのデータセットとまったく異なる外挿というよりは、今の確率密度分布の外側の中でも確率の高いところが探索されることになります。つまり現状のデータセットにおける確率密度分布の方向と一致する方向で探索される可能性が高いことになります。繰り返しになりますが、外挿領域は非常に広いため、現状のデータセットにある程度近い外挿領域とはいえ、想像できないくらい広いです。そのような中でも、GMR や GTMR ではより効果的な外挿領域、データセットから意味のある外挿領域と判断された領域に狙いをつけて、外挿領域を探索するため、結果的に少ない実験回数で目標を達成できると考えられます。
また、GMR や GTMR では X と Y の間の関係、X の関係、そして Y の間の関係が、複数の正規分布の重ね合わせで表現されます。特に GMR では分散共分散行列を自由に決められるため、一つ一つの正規分布が自由度の高い多変量正規分布です。今、解析するのが一つのデータセットであっても、その中には異なるメカニズムで発生するようなサンプルが含まれていると思います。そのメカニズム一つ一つについて、サンプルが正規分布に従うように得られると仮定できれば、メカニズムごとにモデル化することと同じことが、GMR や GTMR によりできることになります。その結果として、直接的逆解析では、メカニズムごと異なったり、もしくは重複したりするようなデータ領域でも、その中でより良好なメカニズムの領域もしくは複合領域を探索できると考えられます。このように、GMR や GTMR ではある程度メカニズムを考慮した探索ができると考えています。
直接的逆解析は、研究室の学生たちも活用しており、いろいろな分野に応用していますし、引き続き研究もしています。またわかったことがあれば報告します。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


