機械学習の手法の中には、カーネル関数を用いた手法があります。サポートベクターマシン、サポートベクター回帰、ガウス過程回帰あたりが有名と思います。
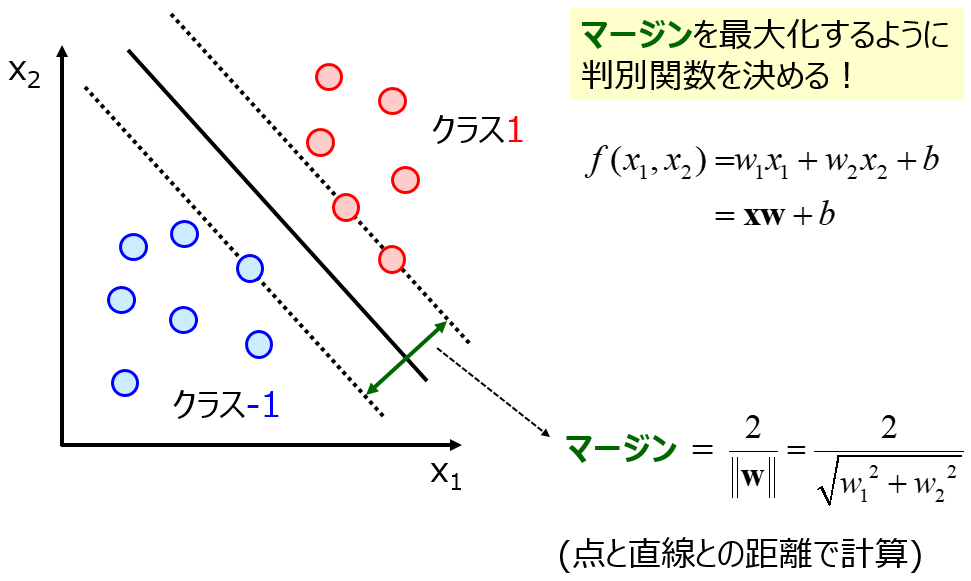


他にもリッジ回帰や主成分分析、独立成分分析など、いろいろな手法とカーネル関数を組み合わせることができます。

なおカーネル関数についてはこちらをご覧ください。

カーネル関数にもいろいろあります。最もよく用いられているのは線形カーネルやガウシアンカーネル (Radial Basis Function (RBF) カーネル) でしょうか。他には、シグモイドカーネルや多項式カーネルなどもありますし、たとえば化学構造の fingerprints などのバイナリの (0 もしくは 1 のみの) 特徴量を扱うときは tanimoto カーネル、サンプルのグラフ構造を扱うときはグラフカーネル、文章などの文字列を扱うときは文字列カーネルを利用できます。
では用いるカーネル関数をどのように選べばよいでしょうか。何にでも使えるベストなカーネル関数があるというわけではなく、データセットによって適したカーネル関数は異なります。回帰分析手法やクラス分類手法において、ベストな手法があるわけではないのと一緒ですね。
カーネル関数を選ぶとき、教師あり学習においては基本的に、新しいサンプルに対する予測精度が高くなるように、カーネル関数を選びたいです。これをふまえて、カーネル関数の選び方は主に 2 つあります。
一つ目は、他のハイパーパラメータと同じように、カーネル関数をハイパーパラメータの一つと考えて、クロスバリデーションにより最適化する方法です。クロスバリデーションについてはこちらをご覧ください。

クロスバリデーションで最適化されたカーネル関数を用いて、テストデータで予測性能を検証しますので、カーネル関数がテストデータにオーバーフィットしないというメリットがあります。一方で、回帰分析手法・クラス分類手法ごとに一つのカーネル関数しか選択されませんので、手法としての多様性 (結果的にトレーニングデータで構築されるモデルの多様性) は小さくなります。たとえば線形カーネルの SVR かガウシアンカーネルの SVR のどちらかしか選ばれないことになりますので、線形SVRと非線形SVRとの間でテストデータの予測精度の比較はできません。多様な手法の中からテストデータを予測できる手法を選ぶことが難しくなります。またハイパーパラメータが増え、その候補の組み合わせが (指数関数的に) 増えます。計算時間もかなりかかることになりますので注意が必要です。
二つ目の方法は、テストデータの予測結果を見てカーネル関数を選ぶ方法です。カーネル関数が異なると別の手法、と考えて、カーネル関数それぞれで、必要に応じてクロスバリデーションでハイパーパラメータを最適化したあとに、トレーニングデータでモデルを構築し、テストデータを予測します。こうすることで、多種多様な手法の中から、テストデータにおける予測精度を見ながらベストなモデルを検討できる、というメリットがあります。また計算時間に関しても、クロスバリデーションで最適化する方法と比べると短いです。しかし色々なカーネル関数からモデルを一つ選ぶことになりますので、結果的にテストデータにオーバーフィットしてしまう危険が出てきます。
以上のように、カーネル関数を選ぶそれぞれの手法で一長一短がありますので、それらの特徴を考慮して、データ解析の背景や目的に応じて使い分けるとよいと思います。
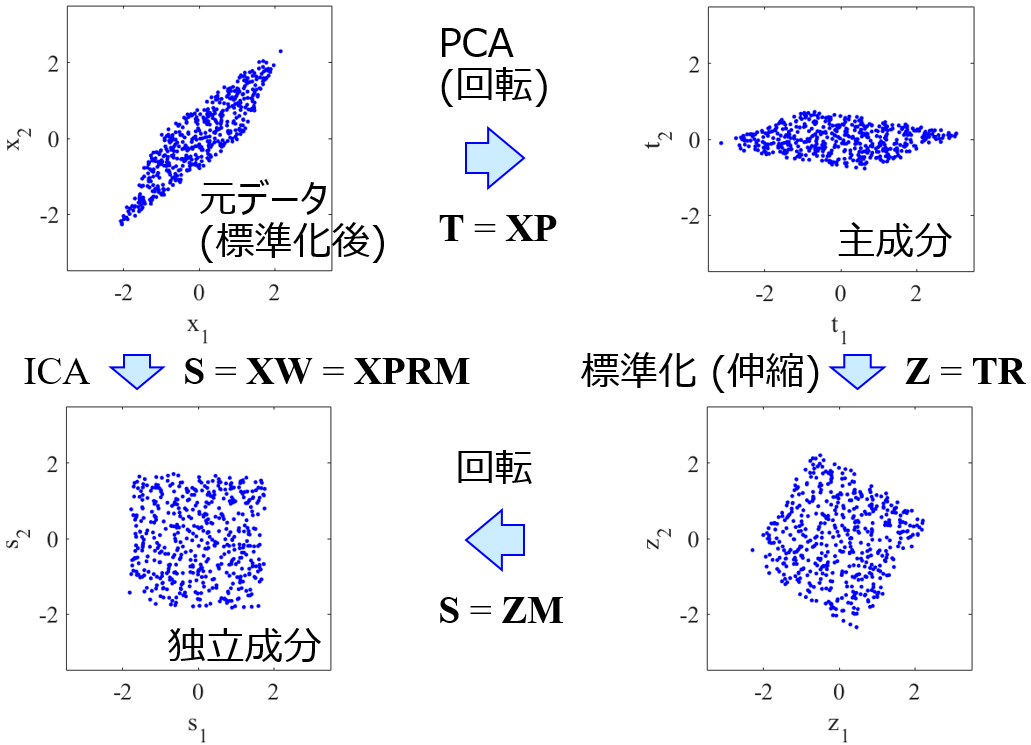
また教師なし学習において、たとえばカーネルPCAやカーネルICAなどのデータの可視化手法に関しては、こちらの k3n-error を用いて選ぶとよいでしょう。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


