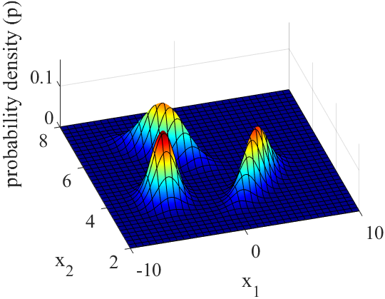
回帰分析やクラス分類では、説明変数 x と目的変数 y があり、x と y の間でモデル y = f(x) を構築します。モデルを用いて、x を入力して y を予測したり、y が目標値になるような x を設計したりします。ここでは、いろいろな特徴量があったときに、x と y に明確に分けてデータ解析が行われます。一方で、扱うデータセットによっては、すべてが x のような扱いだったり、すべてが y のような扱いだったりするケースもあります。すべての特徴量の間の関係性を解析したいということです。
回帰分析やクラス分類では、x と y の間の関係はモデル化できますが、x の間の関係や y の間の関係はモデル化できません。もちろん、すべての特徴量を一つ一つ y にして、それ以外の特徴量を x にして、特徴量の数だけモデルを構築することはできますが、結局は一つの特徴量とそれ以外の特徴量の関係しかモデル化できません。また多くのモデルが存在することになり、モデルの最適化やモデルの管理、そして解析自体が煩雑になってしまいます。
すべての特徴量間の関係を考慮するやり方として教師なし学習があります。低次元化手法やデータ密度推定手法やクラスタリング手法などです。例えば主成分分析によって主成分を計算した後のローディングを見れば、各主成分に対する各特徴量の重みがわかります。

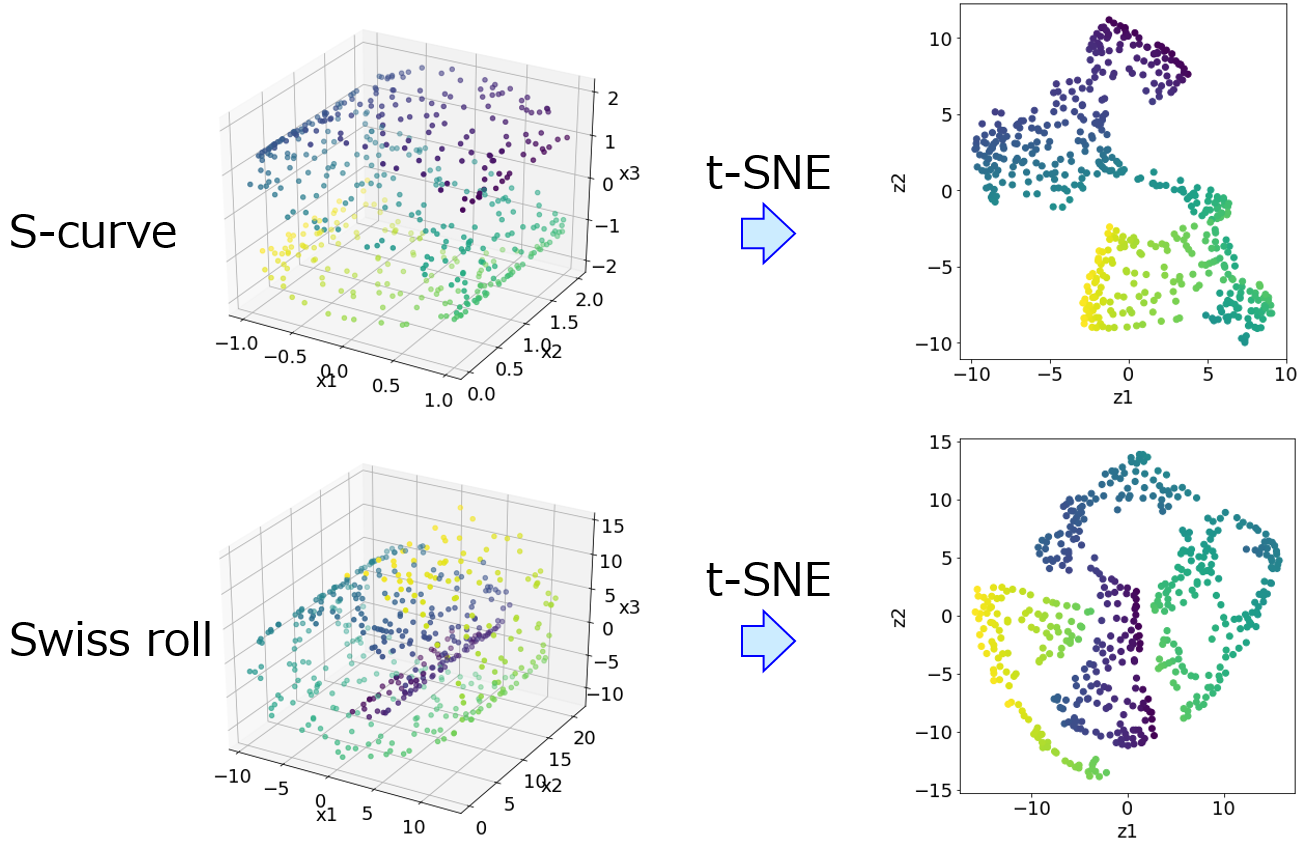
これは特徴量間の関係といえますが、線形の関係に限られていますし、さらにはどの主成分を対象にするかによって重みは変わりますので、任意性も出てきます。t-distributed stochastic neighbor embedding をはじめとする多様体モデルでは、特徴量間の非線形性を考慮することはできますが、そもそも特徴量間の関係を明に表せません。
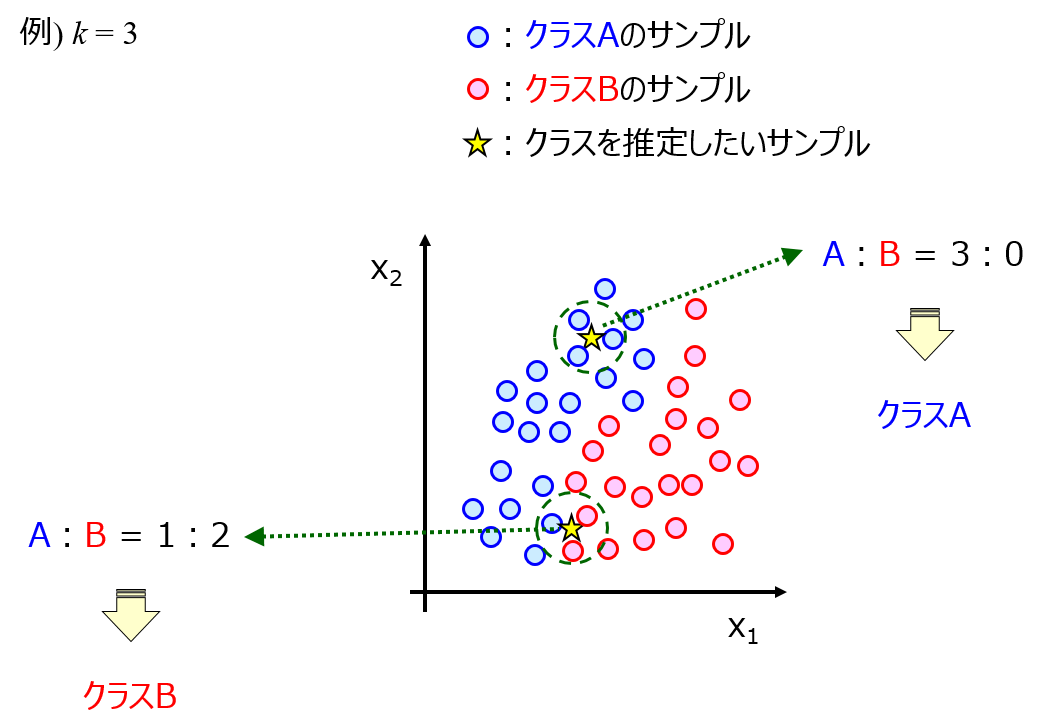
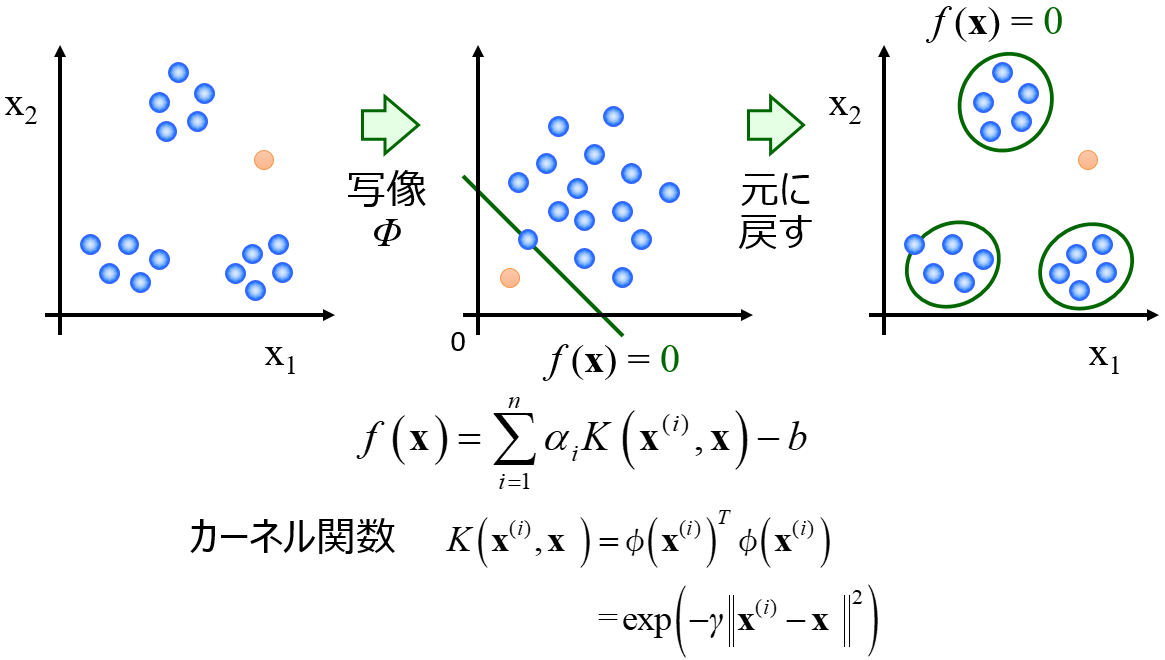
一方、k近傍法や One-Class Support Vector Machine (OCSVM) などベクターマシン御用邸特徴量のすべての得票の行動したデータ密度を計算できます。ただし、すべての特徴量の値をモデルに入力してデータ密度を計算する、といったことはできますが特徴量間の関係を表現することはできません。
以上をふまえて、特徴量間の関係を表現する手法として Gaussian Mixture Model (GMM) をオススメします。
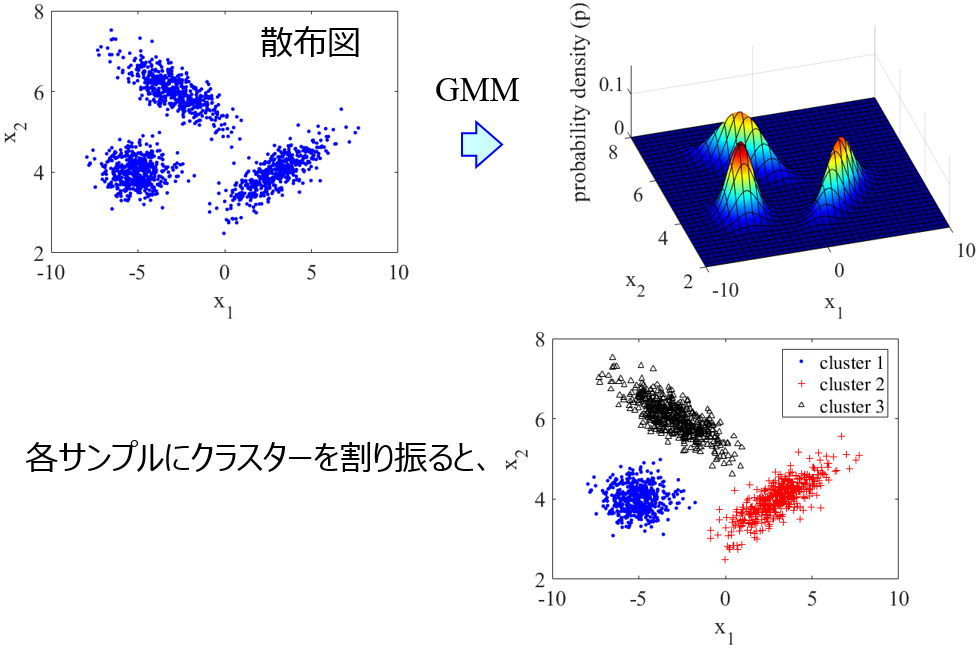
GMM では、特徴量の間の関係が複数の正規分布の重ね合わせで与えられると仮定して、各正規分布の平均や分散・共分散や、正規分布ごとの重みを計算する手法です。なお Generative Topographic Mapping (GTM) も、分散と共分散に制約はありますが、複数の正規分布の重ね合わせでモデルが表現されるため、ここでは GTM も GMM として扱います (以下の議論は GTM でも再現可能です)。GTM では可視化もできるため、分散と共分散に制約はあっても問題ないときは GTM を使用するとよいでしょう。
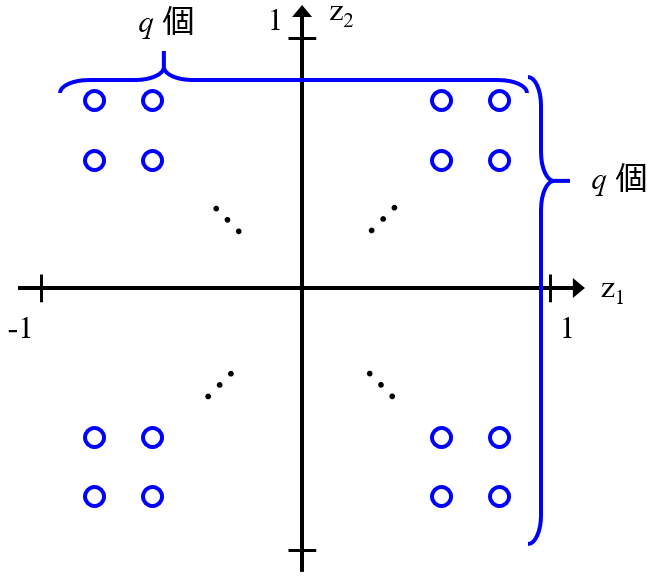
GMM (もしくは GTM) で複数の正規分布の重ね合わせでデータセットが表現されることで、特徴量の間の関係性も求まりますし、確率密度分布であることからデータ密度も計算できますし、さらにクラスタリングの結果、すなわちあるサンプルが各正規分布に所属する割合、も計算可能です。さらには、いくつかの特徴量の値をモデルに入力して、それ以外の特徴量の値を推定する、といったことも、特徴量やその数に限らず自由にできます。つまり回帰分析やモデルの逆解析に相当することも可能です (このあたりは Gaussian Mixture Regression とも呼ばれています)。
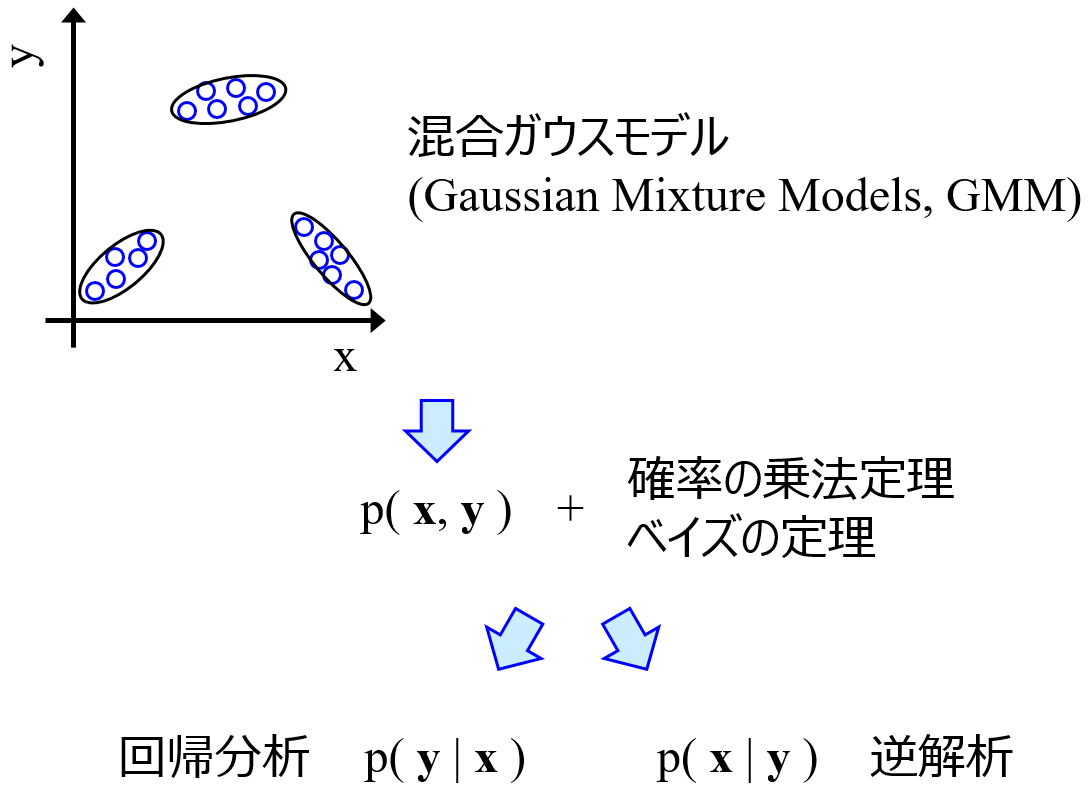
モデルにおける特徴量の関係と、実際のデータとの差異を確認することもできるわけです。このように、GMM では特徴量の間の関係を考慮できることから、補完手法としても使用しています。

もちろん GMM にもデメリットはありまして、複数の正規分布の重ね合わせで特徴量間の関係を表すことが決まっていることから、データセットがその分布に従わないときには適切に関係性を表現することはできません。そのため、データ密度を推定することに限っていえば、k近傍法や OCSVM の方が適切に推定できる可能性はあります。
ただ GMM でしかできないことも多いため、特徴量間の関係を平等に扱って解析したいときや、x やy のある中ですべての特徴量の間の関係をモデル化したいときには、GMM をオススメしています。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。