目的変数 y と説明変数 x のデータを準備して、x と y の間で数理モデル y = f(x) を構築し、モデルに基づいて x の値から y の値を予測したり、y の値が目標値になるような x の値を設計したりします。モデルで予測するとき、基本的にはモデルの適用範囲 (Applicability Domain, AD) を設定し、x の値を入力する前に、それが AD 内か AD 外なのか推定したり、y の予測値のばらつきを計算したりします。

AD 内であれば y の予測値を信用できます。もちろんベイズ最適化のように、あえて AD 外を探索する方法もありますが、

これは実験と x の設計を繰り返し行うことが大前提であり、基本的に AD 外の x の値では y の予測値を信用できません。予測値を信用したいときは、AD 内から探索したり、AD 内の x を予測したりする必要があります。
ソフトセンサーをはじめとする時系列データ解析では、x の設計というよりはむしろ、x の値から y の値を予測し、その予測値を有効活用することが一般的です。予測値を活用するためには、その予測値を信用できないといけませんので、AD を設定したら AD 内か AD 外かが重要になります。もしくは予測値の標準偏差が小さいほど望ましいです。
時系列データの特徴として、時々刻々とデータが増えることが挙げられます。温度や圧力といった簡単に測定可能なプロセス変数のデータだけでなく、測定困難なプロセス変数のデータも、頻度は低いかもしれませんが、着実にサンプルが増えていきます。そのため適応型ソフトセンサー (adaptive soft sensor) のように、新しく測定されたデータを活用してモデルの予測精度を維持、向上させる仕組みもあります。
数理モデルが更新されるのですから AD も更新する必要があります。
もちろん時系列データの AD だからといって特別な方法で設定するといったことはありません。一般的なデータ解析と同様に、上で挙げた URL 先の方法で、k 近傍法や One-Class Support Vector Machine (OCSVM) 等で AD を設定します。
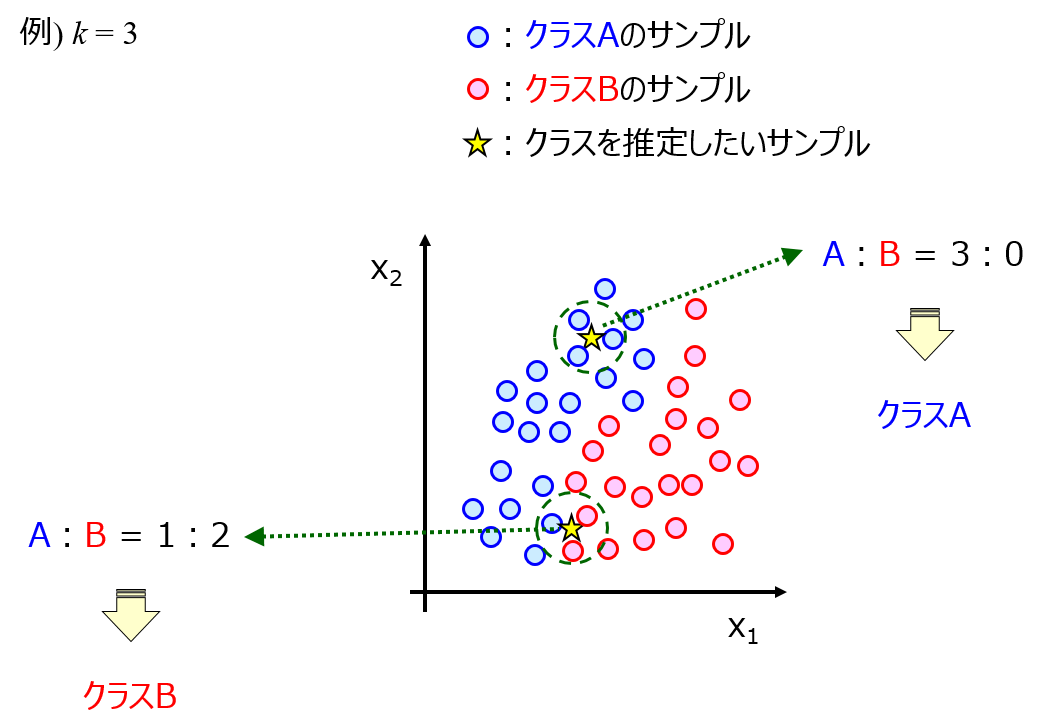
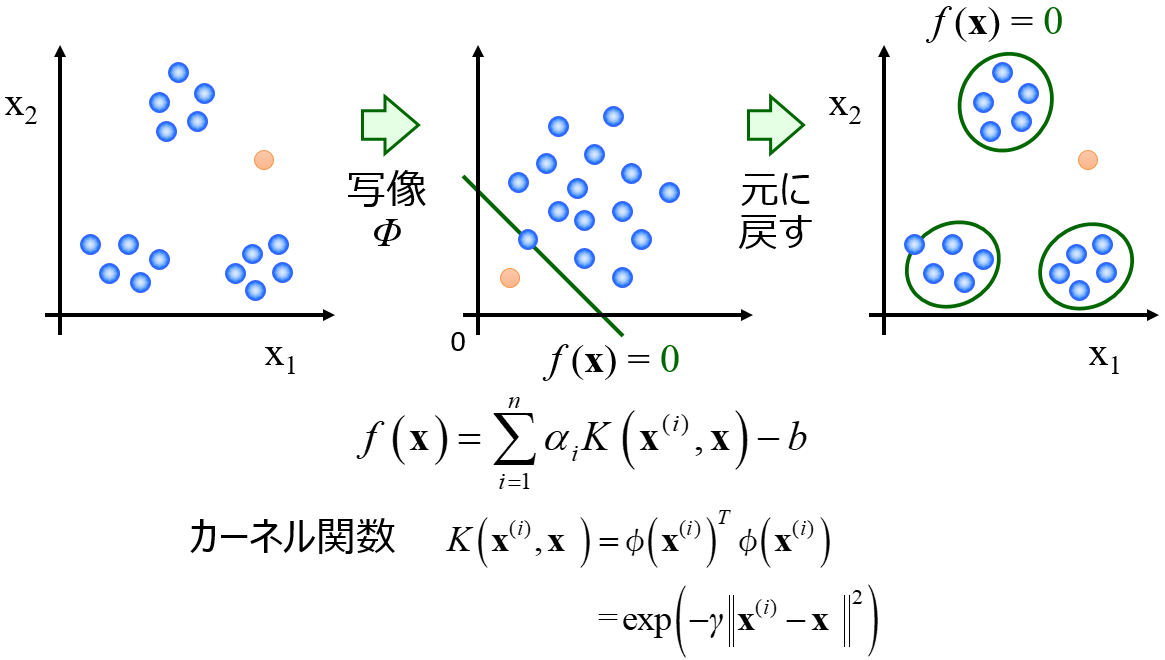
一方で、新たなサンプルが増えたら、そのサンプルをデータセットに追加して再度 AD を準備するとよいです。ただ k 近傍法 の kや OCSVM における ν や γ のようなハイパーパラメータの最適化まで、サンプルが増えるごとに実施する必要はありません。ハイパーパラメータのチューニングまでしようとすると、手間・コストもかかりますし、ハイパーパラメータを自動的に更新したとしても、結果的におかしなハイパーパラメータの値が設定されてしまう可能性もあります。例えば k 近傍法でしたらデータセットにサンプルを追加するだけ OK であり、OCSVM でしたらサンプルを追加した後にモデルを構築することになります。 AD 内と AD 外を分ける閾値を設定している場合は、この閾値もハイパーパラメータとしてとらえて、特に更新する必要はありません。
時系列データの解析をする際は、ぜひ AD を設定するだけでなく、新しいサンプルを用いて AD を更新するようにしてください。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


