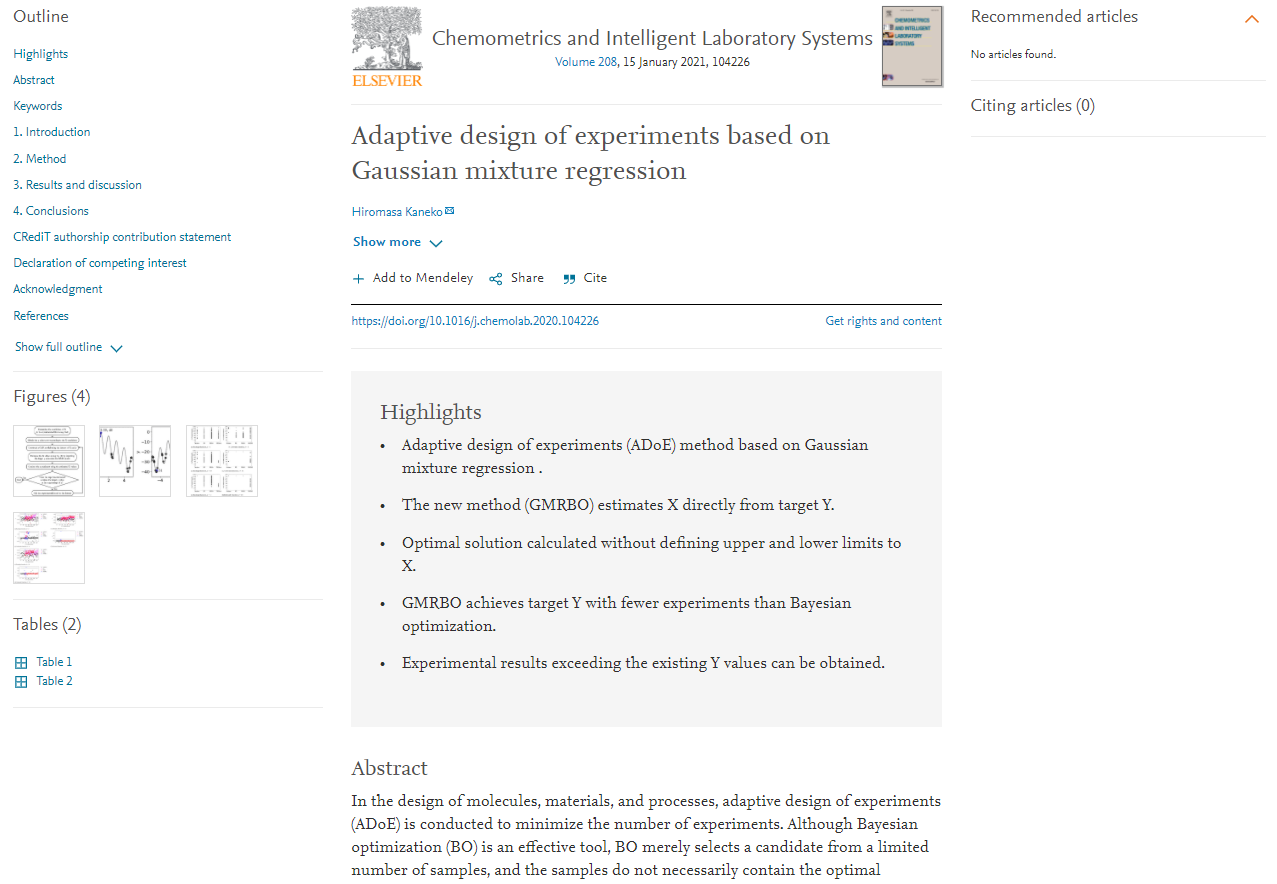
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
x を設計することを考えるとき、大きく分けて3つの逆解析の方法があります。
- y の予測値 + モデルの適用範囲 (内挿、少しの外挿)
- ベイズ最適化 (内挿、外挿)
- 直接的逆解析 (内挿、外挿)
y の予測値とモデルの適用範囲 (Applicability Domain, AD) を組み合わせた方法は、基本的に AD で y の予測値を信頼できる x の範囲で探索することになりますので、内挿もしくは少しの外挿までの探索になります。

ベイズ最適化や直接的逆解析では、外挿も探索できる一方で、回帰分析手法が限定されます。ベイズ最適化はガウス過程回帰 (Gaussian Process Regression, GPR) に限定され、

直接的逆解析では Gaussian Mixture Regression (GMR) に限定されます。
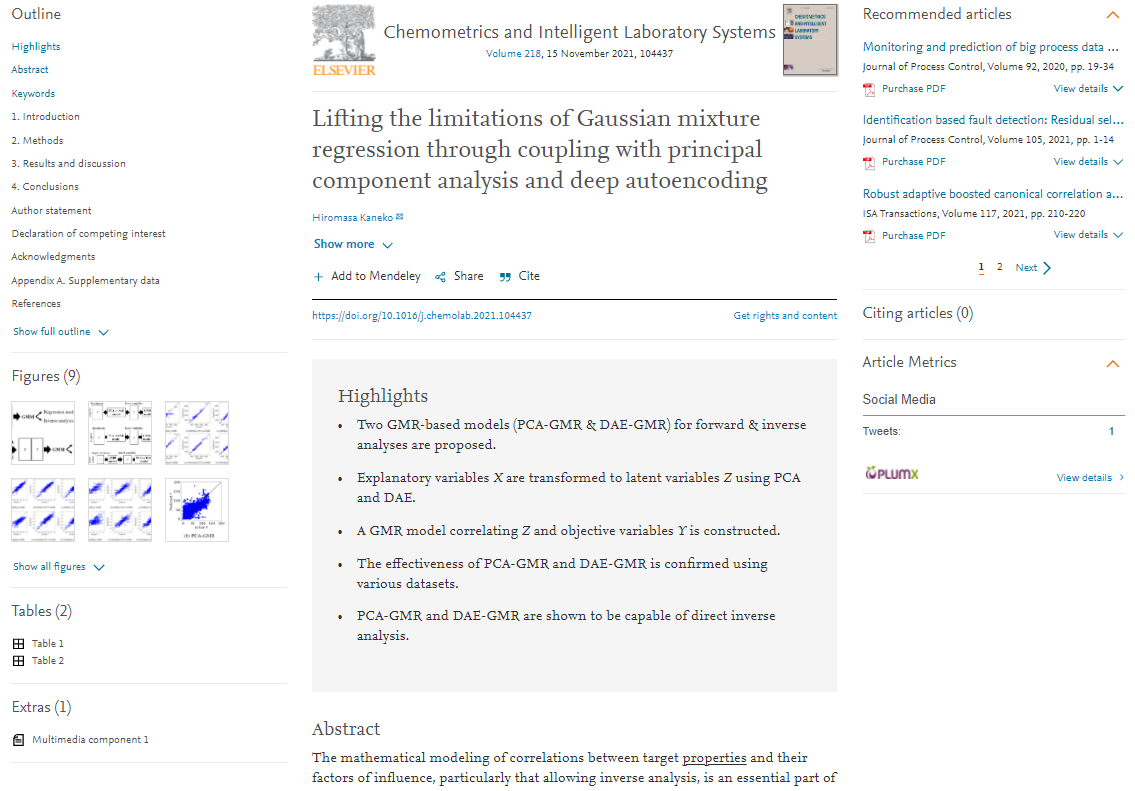
もちろん GPR では色々なカーネル関数があり柔軟な設計ができますし、

直接的逆解析にも GMR に付随する色々な手法があります。
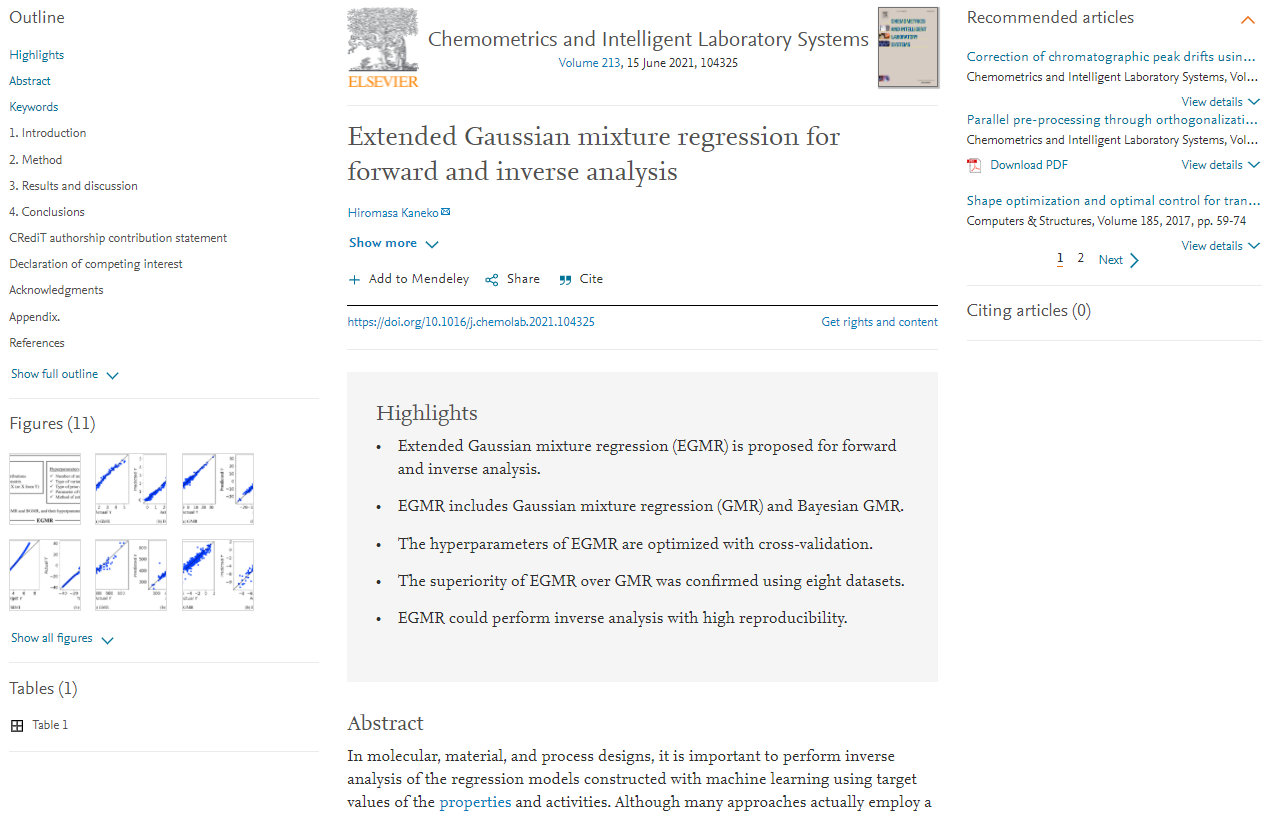
x に制約があるなかでの直接的逆解析も可能です。
まずは、3つの逆解析法すべてに対応できるように、いろいろな回帰分析手法でトレーニングデータ・テストデータの分割やダブルクロスバリデーションでモデルの予測精度を検証しながら、そのデータセットに適切な回帰分析手法を選択すると良いです。
その上で、最適な回帰分析手法でモデルを構築し、y の予測値で AD 内において y の目標値に到達するかどうかを確認します。ここで到達できたら、その x の候補を逆解析の結果にするとよいです。一方で、まだ y の目標値から遠いときには、y の予測値+AD では探索できない外挿を探索する必要がありますので、ベイズ最適化か直接的逆解析を考えます。GPR や GMR の予測精度を考えながら、逆解析を実施します。ただ、x が時系列データの場合など、x 間の関係性も考慮しながら逆解析するには、直接的逆解析一択でしょう。

一方で、次の実験を並行してできる、すなわち複数回の実験ができるときは、実験条件の多様性を考えることも重要です。いろいろな外挿を探索することで、さらに次の実験条件の逆解析に貢献できるためです。そこで、y の予測値 + AD で探索した x の候補、ベイズ最適化で探索した x の候補、直接的逆解析で探索した x の候補すべてを考慮すると、多様な x が得られます。それらを実験することで、次にy の予測値 + AD、ベイズ最適化、直接的逆解析のいずれを行うにしても、より有望な候補を探索できると考えられます。
3つともそれぞれ特徴の異なる手法であり、並行して検討しつつ、場合によっては組み合わせて用いることで、効果的に分子設計・材料設計・プロセス設計を達成できます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。