データ解析とか機械学習とかの話です。こちらの話と関連があります。

たとえば回帰分析で、最小二乗法による線形重回帰分析 (Ordinary Least Squares, OLS) をしたとします。
クロスバリデーションで外部データに対する OLS モデルの推定性能を評価するでしょう。そのときの推定値を用いて、r2, RMSE (Root Mean Squared Error), MAE (Mean Absolute Error) を計算して保存しておきます。
次に、部分的最小二乗回帰 (Partial Least Squares Regression, PLS) をして、OLS とどちらが推定性能の高いモデルを構築できるか、比較します。
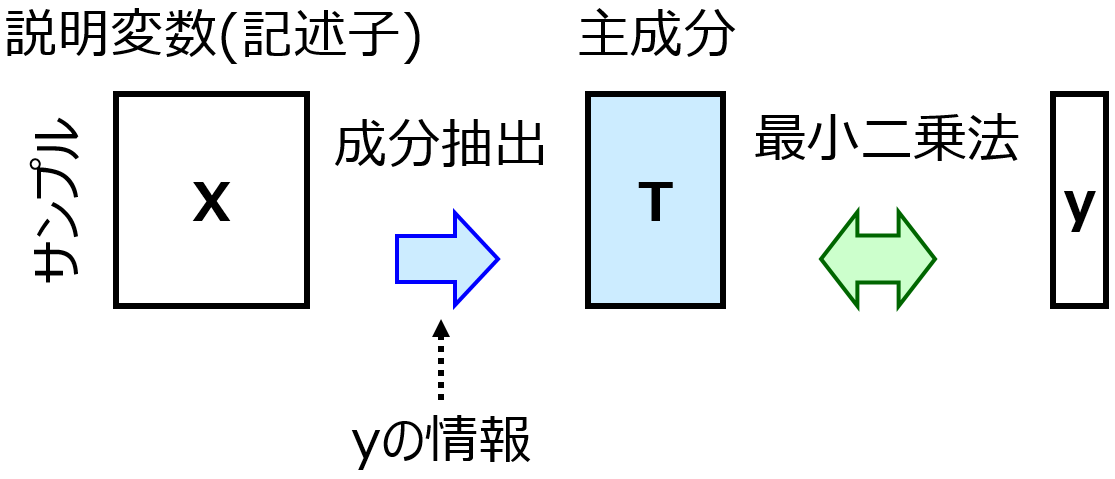
PLS では、成分数を 1, 2, 3, … と変えて、それぞれクロスバリデーションで外部データに対する PLS モデルの推定性能を評価します。クロスバリデーションの fold 数などの設定は OLS のときと同じです。それぞれの成分数でクロスバリデーション後の r2 を計算して、最も r2 が大きな成分数を選び、その成分数で PLS モデルを構築します。
OLS におけるクロスバリデーション後の r2 と、PLS におけるクロスバリデーション後の r2 を比べたとき、PLS の r2 のほうが大きかったとしたら、OLS モデルより PLS モデルのほうが推定性能が高いといえるでしょうか?
残念ながらいえません。PLS では、クロスバリデーションの評価結果を用いて、成分数の最適化をしているからです。PLS で成分数を 1, 2, 3, …, 9, 10 と 10 通りで変えているとすると、PLS では r2 の値が 10 個ある中で、最も高い値を選んでいます。一方、OLS では 1 個しかありません。クロスバリデーションの結果で比較しようとすると、PLS のほうが有利なわけですね。言い方を変えると、PLS ではモデルがクロスバリデーションにおけるバリデーションデータにオーバーフィットしている危険があります。
大事なことは、クロスバリデーションという、推定性能の評価方法が悪いわけではないということです。たとえ、最初にデータセットをトレーニングデータとテストデータに分け、PLS の成分数をテストデータの r2 が最大になるように選んだとしても、同じことがいえます。PLS モデルにおけるテストデータの r2 の値が、OLS モデルの r2 の値と比べて大きかったとしても、PLS モデルの推定性能が高いとはいえないわけです。PLS ではモデルがテストデータにオーバーフィットしている危険があります。
クロスバリデーションでもテストデータを用いた方法でも、ある方法でモデルの推定性能を評価したとしても、その結果で何かを最適化したら、他と比較するための評価にはならないのです。
なので、何か最適化をしたときには、最適化後に、別の方法で再び推定性能を評価する必要があります。たとえば、クロスバリデーションで PLS も成分数を選んだあとに、事前に準備しておいたテストデータで推定性能を評価したり、サンプル数が小さいときには、ダブルクロスバリデーションで評価したりします。
モデルのハイパーパラメータですと、最適化の結果を評価に使わないということは分かりやすいです。しかし他にも変数選択、サンプル選択、外れ値処理や平滑化といったデータの前処理などなど、いろいろなところに最適化は潜んでいて、最適化の結果を評価に使ってはいけないのは見落としがちです。気づかないところで、モデルが何かにオーバーフィットしているかもしれません。注意しましょう!
結局、chance correlation (偶然の相関) の話ということもできます。

モデルの評価しているつもりであっても、これって chance correlation で評価結果がよくなっているだけでは? と感じたら、別の評価方法を考えてみましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


