分子記述子・合成条件・製造条件・プロセス条件・プロセス変数などの特徴量 x と物性・活性・特性などの目的変数 y との間で数理モデル y = f(x) を構築するとき、モデルの予測精度を向上させたり、モデルの解釈性を上げたりするために、x の特徴量選択を行うことがあります。

特徴量選択の手法の中には、数理モデルを構築しながら特徴量を選択する方法があります。モデルを構築するということは、事前にモデルのハイパーパラメータを設定する必要があります。
ただ、それほど難しい話ではなく、基本的にはモデル構築をする際と同様にして、事前にハイパーパラメータを最適化して、それを用いてモデルを構築し特徴量選択することになります。例えば、Least Absolute Shrinkage and Selection Operator (LASSO) による特徴量選択では、λ の候補の中からクロスバリデーションで最適化し、その λ の値を用いた LASSO モデルを構築し、特徴量選択をします。
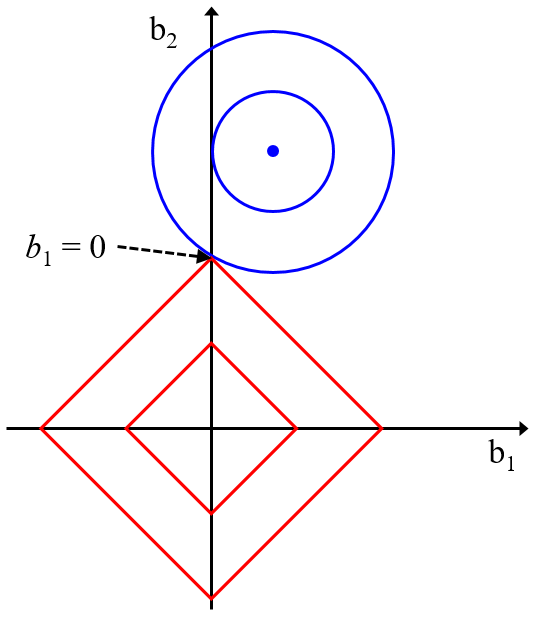
また部分的最小二乗回帰 (Partial Least Squares Regression, PLS) の Variable Importance in Projection (VIP) を用いた方法でも、PLS の成分数をクロスバリデーションで最適化し、その成分数で構築した PLS モデルに基づいて VIP を計算し、特徴量選択をします。
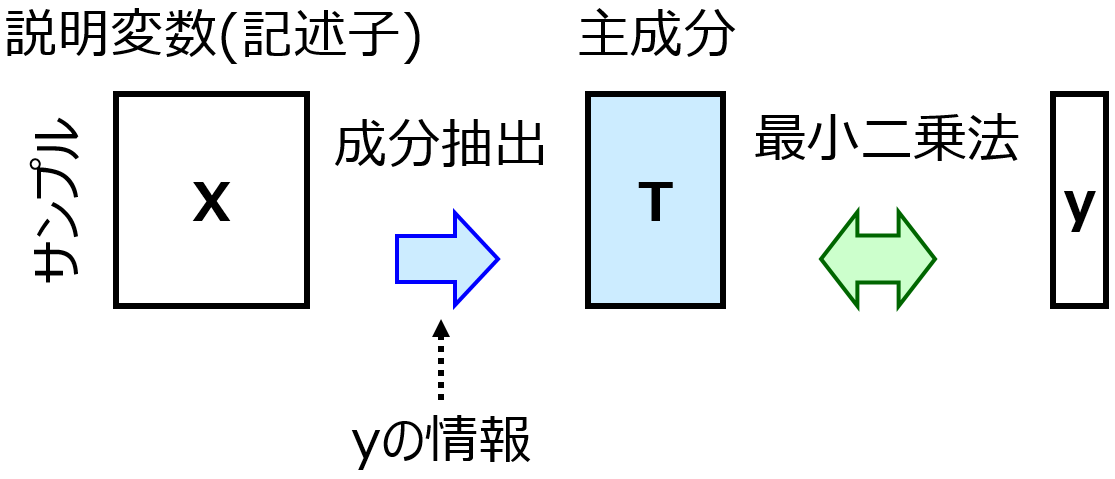
Boruta でも、初めにランダムフォレストのハイパーパラメータを Out-Of-Bag (OOB) によって最適化し、それを使用します。

一方で、遺伝的アルゴリズム (Genetic Algorithm, GA) に基づく特徴量手法では、モデル構築をするごとにハイパーパラメータを設定することが簡単にできます。例えば GAPLS のように GA の繰り返し計算の中で、クロスバリデーションで PLS の主成分を最適化したり、GASVR のように GA の染色体に特徴量の選択に関する情報だけでなくハイパーパラメータの情報を入れることで、特徴量とハイパーパラメータを同時に最適化したりすることもできます。このあたりは計算時間との兼ね合いで決めるとよいでしょう。
以上のように、基本的にはモデルを構築する前にハイパーパラメータを最適化するだけで OK ですが、特徴量を選択する中でハイパーパラメータの最適化を含めることが可能なときは、ぜひ検討するとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


