分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
モデルを構築するとき、組成や収率など y の範囲が 0 から 1 の間だったり、0 から 100 の間だったりするデータセットを扱うことがあります。さらに 0 のサンプルが多かったり、1 のサンプルが多かったりするとき、回帰分析でテストデータを予測したりダブルクロスバリデーションをしたりすると、y の実測値 vs. 予測値プロットにおいて、y の実測値が 0 や 1 (100) のところにサンプルが縦に並ぶことがあります。イメージはこんな感じです。
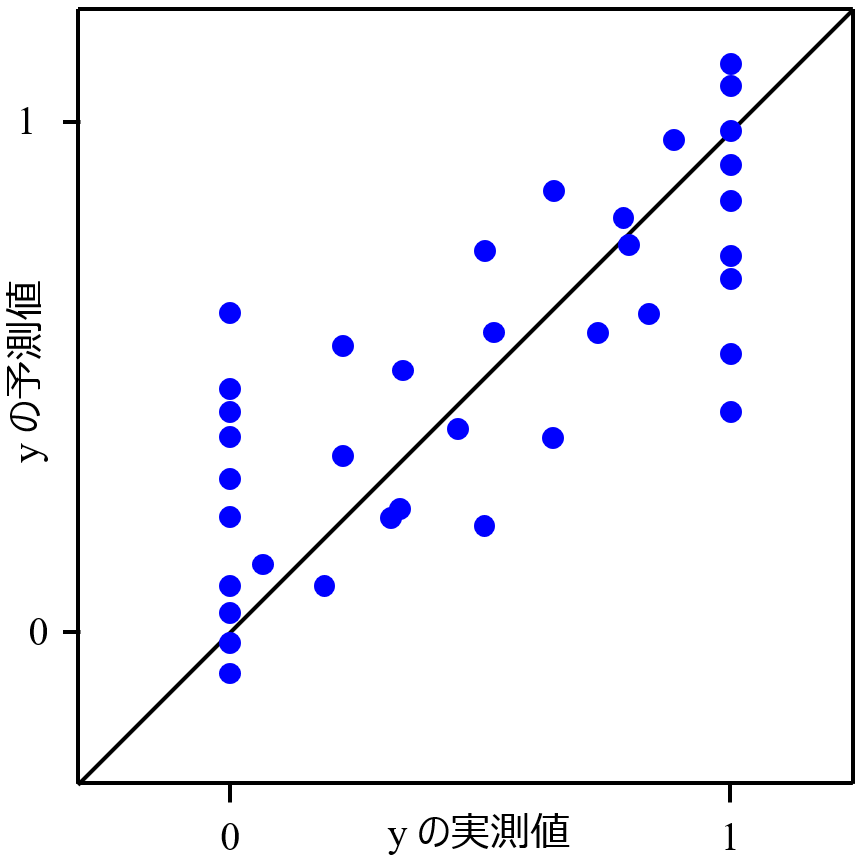
このとき、基本的な考え方としては、こちらに書いたようにサンプルのバランスを整える、すなわち 0 のサンプルや 1 のサンプルをいくつか削除して数を減らしても全体の予測誤差が小さくなることはありません。

ただ例外もあります。
それは、例えば y が 0.1 のような小さい値のときと、y が (正確に) 0 であるときで、y の値が発現するメカニズム、もしくは x と y の関係が異なるようなときです。例えば y が収率のとき、収率 0 はまったく反応が進行していませんが、0 より大きな値であれば、反応は進行しています。このとき、反応がいく場合といかない場合でメカニズムが異なると考えることもできますし、同じ y が 0 のサンプルを全て一緒のものとして扱わないほうがよいかもしれません。
このようなとき、可能であれば、上限・下限がないような y に、化学的・物理的な背景に基づいて、変換できるとよいです。収率を活性化エネルギーにするイメージです。こうすることで、同じ収率 0 のサンプルでも、活性化エネルギーの高さで差別化できる可能性があります。
y の変換が難しいときはどうすればよいでしょうか。
このとき、y が 0 のサンプルや 1 サンプルをすべて削除することで、それ以外のサンプルの予測精度が向上する、すなわち実測値 vs. 予測値プロットにおいて 0 や 1 以外のサンプルが対角線に固まることもあります。y が 0 や 1 以外の値をもつ、y の値が発現するメカニズムが同じであったり、x と y の関係を統一的に表現可能だったりするサンプルのみでモデル構築をすることで、的確にモデル化しようとします。
では、分子設計・材料設計・プロセス設計において、y が 0 や 1 の値をもつサンプルを設計したい場合はどうすれば良いでしょうか。y が 0 や 1 の値をもつサンプルが欲しいとき、y が 0 から 1 の間の予測精度がいくら上がっても、0 や 1 であることを予測できないと意味がありません。ただ一方で、y が 0 や 1 の値をもつサンプルをデータセットに入れると、予測精度が低下する恐れがあります。
このときは、クラス分類と回帰分析を組み合わせるとよいでしょう。例えばy が 1 の値をもつサンプルを設計したいとき、y が 1 の値をもつサンプルをクラス “1” のサンプル、それ以外のサンプルをクラス “0” のサンプルとして、”1” or “0” のクラス分類をします。そして構築したクラス分類モデルを用いて、”1” のクラスになるサンプルを設計します。
さらに、クラス ”0” と予測されたサンプルは、y が 0 や 1 の値をもつサンプル以外で構築した回帰モデルを使うことで、y が 0 から 1 の範囲の中でどの値なのかを予測できます。例えば y が複数あり、基本的にすべての y が 1 になって欲しい一方で、それは難しく、y すべてをなるべく 1 に近づけたいときに、クラス分類と回帰分析を併用するやり方が有効です。
他の場合として、y が 0 以外の小さい値のときと 0 であるときとで y の値が発現するメカニズムが同じであったり、x と y の関係は統一的に表現できたりすると仮定できるとき、0 付近や 1 付近の予測精度を上げたい場合には、0 を 0 以外のサンプルの最小値の 1 / 2 で置き換え、1 を 1 以外のサンプルの最大値と 1 の間の平均値で置き換えた後、ロジット変換することで、
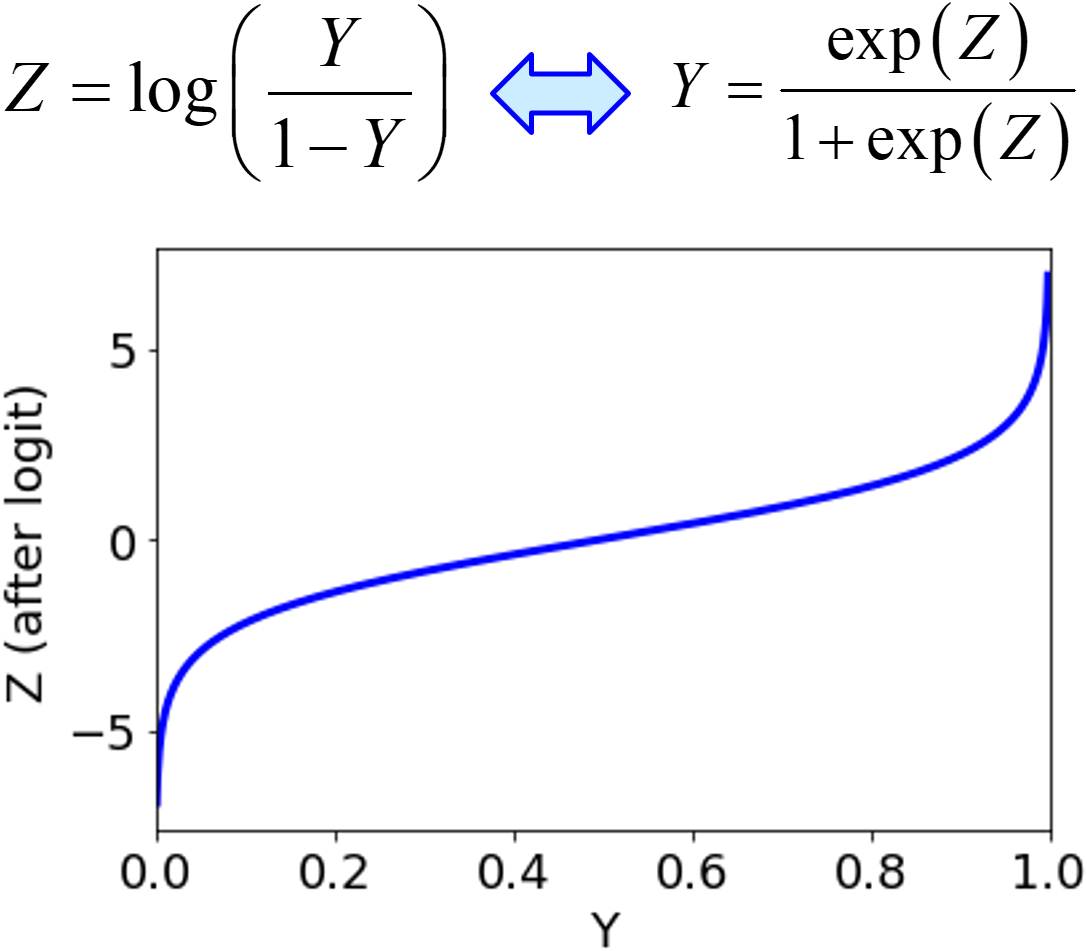
予測精度を向上させることもできます。ご参考になれば幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。
