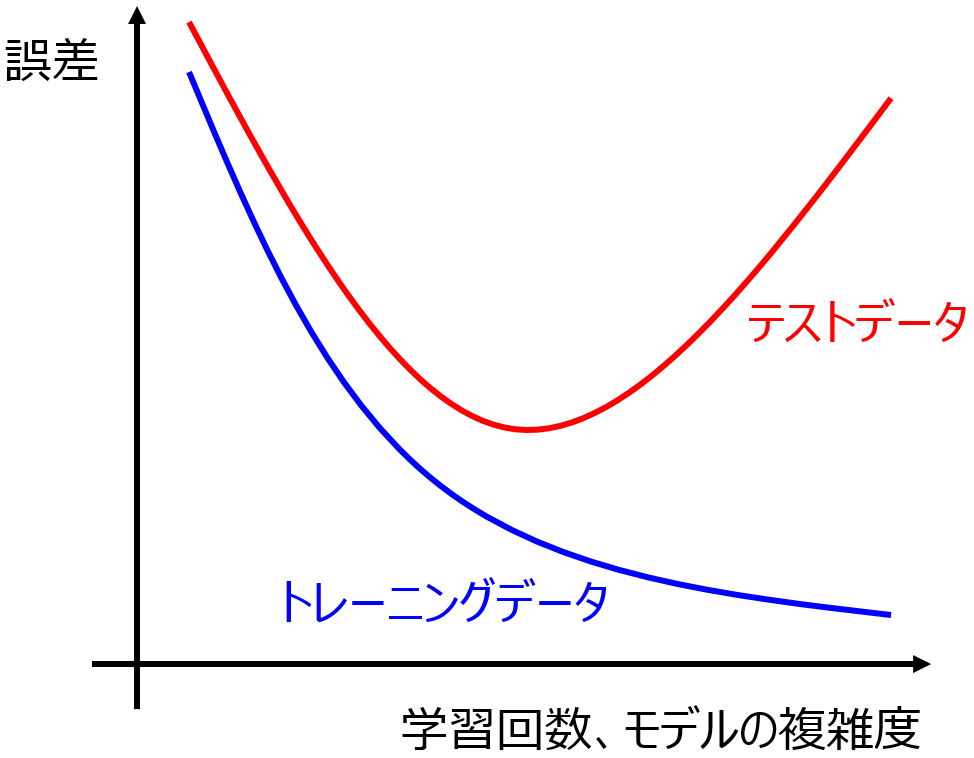
オーバーフィッティングについて考えます。オーバーフィッティングは予測精度の高いモデルを構築するときの問題でして、モデルがトレーニングデータに合いすぎてしまい (目的変数 y の推定誤差が小さくなりすぎてしまい)、新しいデータにおける目的変数 y の誤差が大きくなってしまうことです。詳しくはこちらをご覧ください。
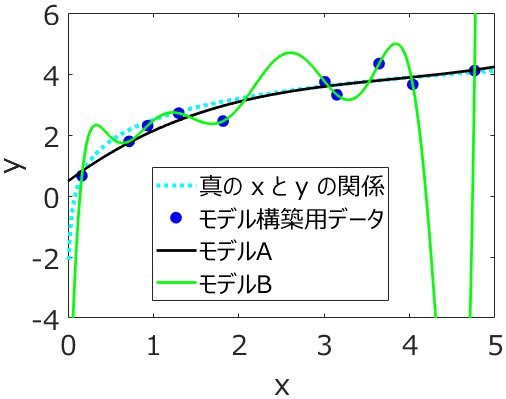
たとえば、説明変数 x の数を増やしたり、PLS モデルにおける主成分の数を増やしたりすると、モデルは複雑になります。複雑になることで、よりトレーニングデータにフィットするようになります。y の誤差が小さくなるわけですね。
このとき、たとえば y の実測値に含まれる測定誤差などのノイズが事前にわかり、そのノイズよりもトレーニングデータの y の誤差が小さくなっていたら、モデルがオーバーフィッティングしているといえるでしょう。
でも、データに含まれるノイズがわからないときは、オーバーフィッティングしているかどうか誰にもわかりません。
ここでテストデータを用います。テストデータの y の値を推定したときに、どのくらいの誤差で推定できたかをチェックするわけです。トレーニングデータにおける y の誤差より大きいときには、モデルはオーバーフィッティングしていると考えられるでしょう。よく出てくる下のような図において、
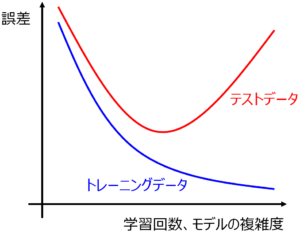
テストデータにおける y の誤差がもっとも小さくなるようなモデルがいいよね、といった感じです。ここで、上の図における赤線はテストデータの結果であり、y の値が未知のデータに対する推定性能である汎化性能とは似て非なるものであることに注意する必要があります。実際、汎化性能は誰にもわからず、基本的にはテストデータに対する性能と仮定してしまいます。
ちなみに、トレーニングデータ (青線) もテストデータ (赤線) も両方誤差が大きい、図の左のあたりをアンダーフィッティングとよびます。ただ、基本的にモデル構築手法がトレーニングデータの y の誤差を小さくすることを目指しており、バリデーションデータを使用する方法やクロスバリデーション等の適切な方法でハイパーパラメータの最適化をできることから、アンダーフィッティングについてはそれほど気にしなくてもよいでしょう。
モデルを構築するとき、基本的には汎化性能の高いモデルを目指します。できることとしては、テストデータの推定性能が高いようなモデルを選ぶことです。
このとき、テストデータの推定性能が低い場合に、ぜんぶ全部オーバーフィッティングのせいだ。とシンプルにしてしまっても問題ないと思います。
基本的にテストデータのサンプルはランダムに選びます。ある程度サンプル数が大きいときは、テストデータとしてのサンプルがまんべんなく選ばれますし、Kennard-Stoneアルゴリズムで意図的にまんべんなく選択することもできます。サンプル数が小さいときは、ダブルクロスバリデーション

において外側のクロスバリデーションを leave-one-out クロスバリデーションにして検証できます。なので、トレーニングデータとテストデータのデータの偏りについては、考慮しなくてもよいと考えます。
もちろんデータが偏ることもあります。たとえば、時系列データを扱うときなどです。ある時刻までのサンプルをトレーニングデータ、それ以降の時刻のサンプルをテストデータとします。新しい時刻におけるプロセス状態がそれ以前のプロセス状態と異なるとき、テストデータはトレーニングデータとは別のデータ分布になる可能性があります。このようなテストデータにおける y の推定誤差が大きくなってしまうときも、オーバーフィッティングとしてしまってもよいと思います。結局、トレーニングデータにおける y の誤差を小さくするようにモデルを構築して、トレーニングデータによく当てはまる一方で、テストデータを予測できなかった、というわけです。オーバーフィッティングとしてもよいでしょう。そしてこれを軽減するためにいろいろと工夫しようというわけです。
他にもテストデータにおける y の推定誤差が大きくなる原因は色々と考えられますが、オーバーフィッティングとしたほうがシンプルでよいと思います。そしてこのオーバーフィッティングに対して対策を考えます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。