以前に、半教師あり学習 (半教師付き学習) における4つのメリットについて書きましたが、

その中で回帰分析におけるメリットを議論して、それをQSAR解析・QSPR 解析で確認した論文が、掲載されましたのでご紹介致します。
金子研オンラインサロンでは、別途論文を共有します。
ここで対象としたのは、
- 教師ありデータ + 教師なしデータ で次元削減をして、
- 次元削減後の空間において、y との間で回帰分析を行う
手法です。図で表すと下のようになります。
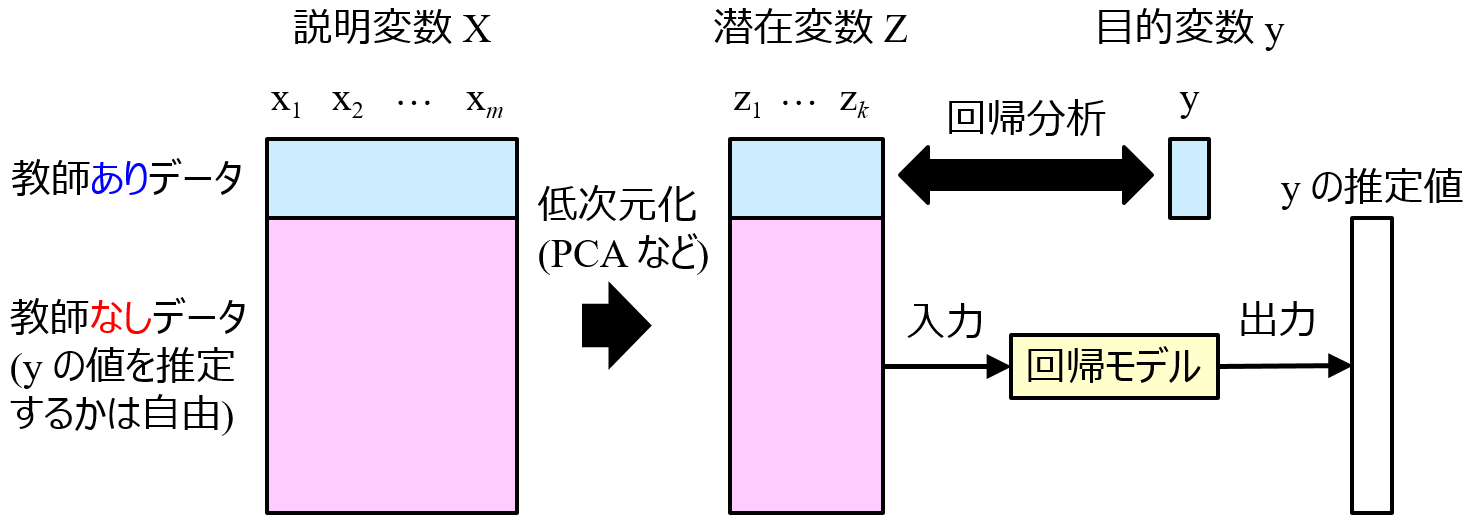
X と y との間で回帰モデル y = f(X) を構築するのではなく、教師ありデータ + 教師なしデータを用いて低次元化した潜在変数 Z と y との間で回帰モデル y = f(Z) を構築します。
低次元化の手法としては、線形手法の主成分分析 (Principal Component Analysis, PCA) と 非線形手法のLocally Linear Embedding (LLE) で検討しています。ただ、もちろん Generative Topographic Mapping (GTM) や t-distributed Stochastic Neighbor Embedding (t-SNE) を用いることもできます。
このような半教師あり学習により、
- モデルの安定性が向上する
- モデルの適用範囲が広がる
わけです。教師ありデータだけで次元削減するよりも、教師ありデータと教師なしデータとを合わせて次元削減したほうが、潜在変数が安定することが確認できました。また、そのような潜在変数空間においてモデルの適用範囲 (Applicability Domain, AD)

を決めることで、従来と比べて AD が広くなりました。
ただ、潜在変数の数 (PCAにおける主成分の数) をいくつにするか、教師なしデータをどのように選択するか、といった課題は残っています。
興味のある方は、論文をご覧になっていただけると幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。