変数選択・特徴量選択の手法はいろいろあります。同じ値をもつサンプルの割合が大きい特徴量を削除したりとか、相関係数の絶対値が大きい特徴量の組の一つを削除したりとか、

モデルの予測精度を高めるように特徴量を選択したりとか、


乱数の特徴量のような目的変数と関係ない特徴量を削除したりとか

いろいろです。
その中で、モデルの予測精度を高めるような特徴量選択、というのはとても魅力的です。ただ、特徴量選択で高めることのできるモデルの予測精度とは何なのか、把握しておいた方がよいです。というのも、ここでのモデルの予測精度というのは、広い意味での内部バリデーションの結果としての予測精度だからです。たとえば、stepwise や GAPLS, GASVR といった特徴量選択手法において、クロスバリデーションにおける予測結果がよくなるように特徴量を選択することがあります。これにより、すべての特徴量を用いたときよりも、クロスバリデーション後の r2 が高くなることが多いです。この特徴量選択では、クロスバリデーションにおける予測結果をモデルの予測精度といっているわけです。しかし、クロスバリデーションにおける予測結果が向上したからといって、必ずしも新しいサンプルに対する精度が高くなるわけではありません。クロスバリデーションの結果に、特徴量セットがオーバーフィット
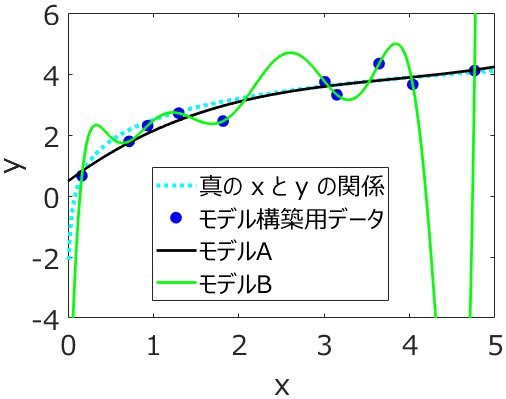
している可能性があります。
では、クロスバリデーションではなく、別途バリデーションデータを準備して、その予測結果がよくなるように、つまりバリデーションデータの r2 の値を大きくするように、特徴量を選択すればよいのでしょうか。この場合、バリデーションデータに特徴量セットがオーバーフィットする危険が高まるだけで、本質的な解決にはなっていません。そもそもクロスバリデーションは、外部バリデーションを繰り返すことです。特徴量選択において向上できるモデルの予測精度とは、今あるデータセットで計算できる予測精度であり、広い意味での内部バリデーションにおける予測精度なのです。
基本的に、データセットにおける特徴量の数は大きいことが多いです。そのような非常に自由度の高い中で、特徴量セットを最適化することになりますので、最適化に用いたサンプルに、特徴量セットがオーバーフィットする可能性が高いわけです。特にサンプル数が小さいときには、とても注意が必要です。


対処法としては、たとえばクロスバリデーションの fold 数 (分割数) を小さくしたりとか、外部データのサンプル数を大きくしたりとかです。また、目的変数の情報を使わずに、事前に特徴量を選択しておく (自由度を減らしておく) こともあります。同じ値をもつサンプルの割合が大きい特徴量を削除したりとか、相関係数の絶対値が大きい特徴量の組の一つを削除したりとかですね。目的変数の情報を使わない、というのが重要でして、用いるとオーバーフィットの危険が出てきてしまいます。他には、PLS の最適成分数の上限値を小さくするなど、モデル構築手法における自由度を小さくするのも一つの手です。波長選択をするときや、時系列データにおける時間遅れを選択するときには、選択する領域の数を小さくすることもよいでしょう。
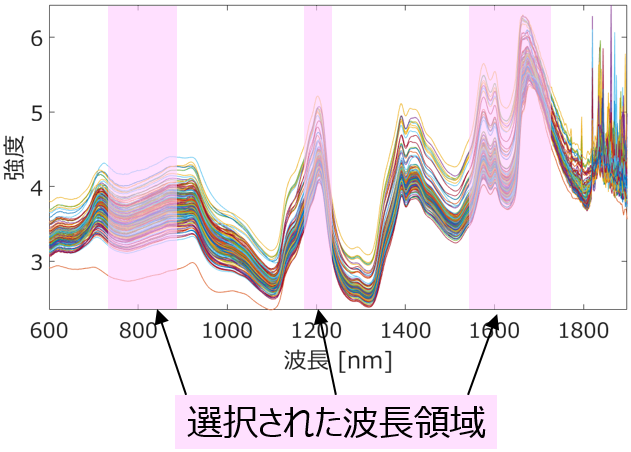
以上のように、モデルの予測精度を高めるタイプの特徴量選択手法を用いるときは、今あるデータセットに特徴量セットがオーバーフィットしないよう工夫して、用いるとよいでしょう。ただ、どんな工夫をしても、オーバーフィットを避けられないこともありますので、その場合は他のタイプの特徴量選択手法を用いるのがよいと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


