半教師あり学習 (半教師付き学習) に関する、金子研学生との共著論文が Chemometrics and Intelligent Laboratory Systems に掲載されました。半教師あり学習のメリットはこちらに書いたとおりでして、

実際に確認もしています。
特に、教師ありデータ (目的変数 y の値がそろったデータ) と教師なしデータ (y の値がないデータ) とを合わせてから主成分分析 (Principal Component Analysis, PCA) で成分 (潜在変数) を抽出し、教師ありデータにおいて PCA 後の成分と y との間で回帰モデルを構築する Python コードはこちらにあります。
実はこれだけでは問題なこともありまして、、、教師なしデータのなかに外れたサンプルがあると、かえって回帰モデルの推定性能を低下させてしまう!!、のです。これまで基本的には、教師なしデータが与えられたとき、それらすべて (と教師ありデータ) を用いて、PCA を行っていました。でも、教師なしデータに外れサンプルがあると、PCA 後の主成分が外れサンプルを表現するためのものになり変な感じになってしまいます。
なので、外れサンプルは事前に検出しておくとよいです。ただ、教師なしデータなので、こちらの手法

では、外れサンプルを検出できません。
与えられた教師なしデータの中から、PCA に用いるサンプルを選択するにはどうしたらよいか。今回の論文では、モデルの適用範囲 (Applicability Domain, AD)

に着目しました。
教師ありデータで AD を決めて、AD 内の教師なしデータのみ、PCA に用いるようにしました。サンプルコードはこちらにあります。
[NEW] DCEKit で便利に半教師あり学習や AD によるサンプル選択を利用可能です。scikit-learn に準拠したモデルになっていますので、cross_val_predict, GridSeachCV なども利用可能です。デモンストレーションもあります。

論文では、QSPR, QSAR 解析を通して、今回の手法で回帰モデルの推定性能が向上することを確認しています。
実は論文においては、もう一歩ふみこんだサンプル選択をしています。キーワードとしてはベイズ最適化です。
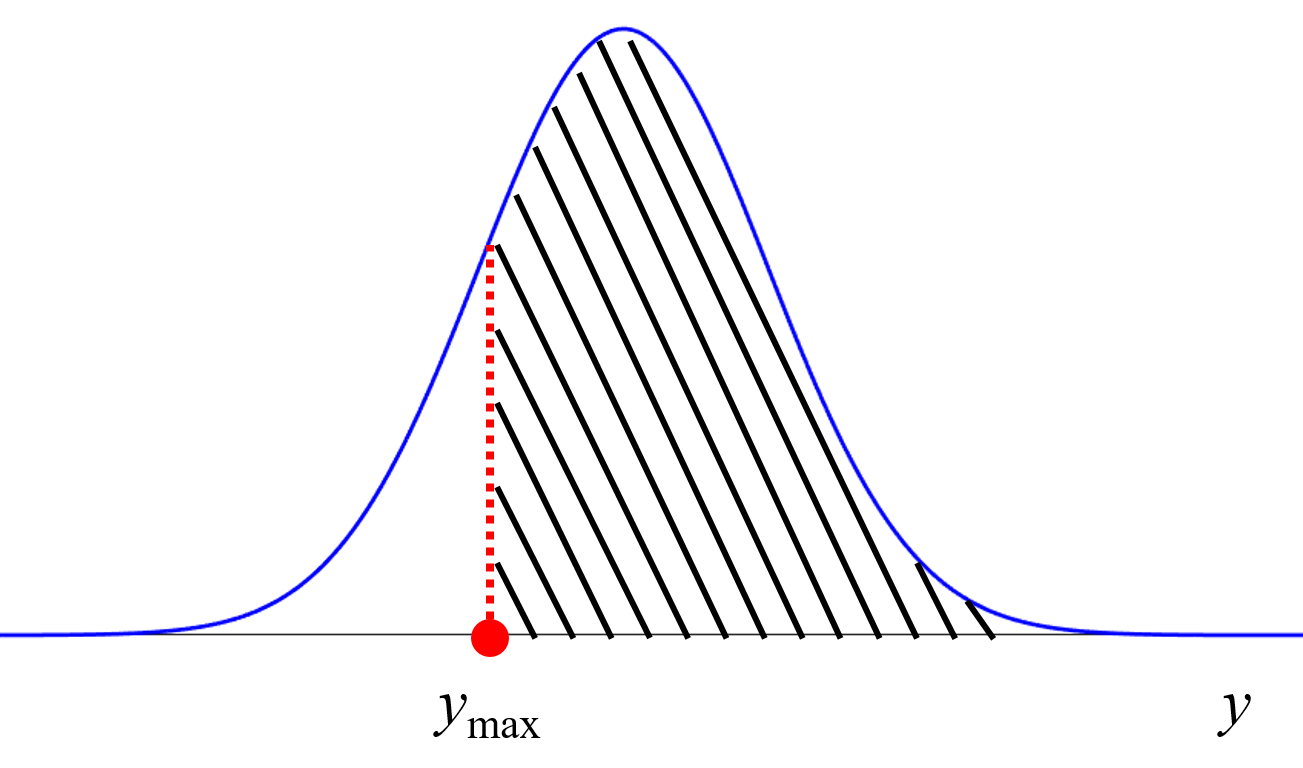

回帰モデルを分子設計や材料設計に用いるときには、目的変数の値の目標値、もしくは目標範囲があります。目的変数の値が大きいような、もしくは小さいような、分子を設計したい、材料の実験条件・製造条件を設計したい、といった感じです。
なので、回帰モデルの推定性能を向上させることが目的なのはもちろんですが、目的をしぼると、目標範囲における回帰モデルの推定性能を向上させたい!!、になるわけです。そこで、ガウス過程による回帰

により、教師なしデータのサンプルそれぞれが、目標範囲を満たす確率を計算し、その確率が高いサンプルのみ選択して、PCA に用います。論文では、QSPR, QSAR 解析で目的変数の目標範囲における回帰モデルの推定誤差が小さくなることを確認しています。
論文はこちらです。こちらからは、2019 年 8 月 21 日まで無料で読めます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。