回帰分析やクラス分類をする前の、データセットの前処理の話です。2 つの説明変数 (記述子・特徴量) の間で、相関係数の絶対値が大きいとき、それらの変数は似ているということです。余計な変数は、回帰モデル・クラス分類モデルに悪影響を及ぼすため、どちらか 1 つの変数を削除します。
もちろん、たとえば PLS
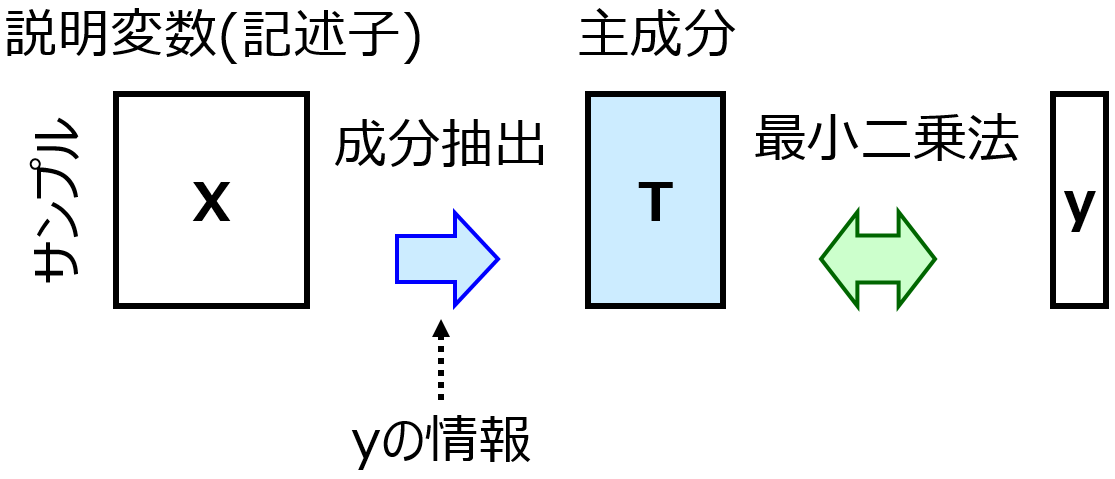
をすれば説明変数 → 互いに無相関な成分 に変換できますので、いわゆる多重共線性 (multicollinearity, マルチコ) には対処できます。ただ、特にサンプルが少ないときなど、chance correlation (偶然の相関) の問題

もありますので、事前に説明変数の数を減らせるなら、それが望ましいです。
こんな論文もあります。
記述子選択の論文。相関係数の絶対値が大きい記述子の組の一方を削除して、MLRでモデル構築。活性・ADME・毒性の4つのデータセットで検証したところ、相関係数の絶対値 0.8 では削り過ぎで、0.95から0.9999の間が適当。それでも多くの記述子を削減可能https://t.co/OCT2WKm4bu
— 金子弘昌/Hiromasa Kaneko (@hirokaneko226) 2019年6月15日
そこで、説明変数の間の相関係数にもとづいて、変数を削減しましょう。1 つのやり方は、相関係数の絶対値が最大となる変数の組における 1 つの変数を削除することを繰り返します。相関係数の絶対値が、しきい値未満になったら終了です。変数の組における 1 つの変数をどのように選ぶかは、他の変数との相関係数の絶対値の和が、大きい方を選ぶとよいでしょう。
もちろん、説明変数の数を減らすだけなら、この方法で問題ありません。相関係数の絶対値がしきい値以上の変数の組み合わせはなくなります。ただし、機会的に変数が削除されてしまうため、構築した回帰モデル・クラス分類モデルの解釈をしたい場合は、ちょっと困るかもしれません。ある変数が重要、と解釈されても、もともとその変数と相関の高い変数があったかもしれません。そのような相関の高かった変数は重要とは判断されません。また説明変数の値を設計したいときにも、適当に変数が削除されても困りますね。
最終的に変数の解釈をしたり変数の値を設計したりしたいときに、困らないようにするためには、相関係数の絶対値を用いて変数をクラスタリングするとよいでしょう。たとえば、最遠隣法による階層的クラスタリングが、さきほどの相関係数の絶対値が最大となる変数の組における 1 つの変数を削除することを繰り返す方法と近いです。クラスタリングしたあとは、しきい値にもとづいて具体的なクラスターを決めて、クラスターごとに適当に 1 つの変数を選択するか、クラスター内の変数をすべてオートスケーリング (標準化)

してスケールをそろえたあとに、変数の平均値を新しい変数にするとよいでしょう。PCA

をして第 1 主成分を用いるのがよいのかもしれませんが、、、高い相関があることですし平均値で十分でしょう。
相関係数で変数を処理する Python コードを公開します。こちらにありますのでご自由にお使いください。
メインの関数は variable_selection_based_on_r.py にありますが、その使い方を確認するために、2 つのデモのプログラムを実行するとよいでしょう。1 つ目の、相関係数の絶対値の大きい順に、相関の高い 2 つの変数の一方を削除するプログラムは、 demo_of_searching_highly_correlated_variables.py です。threshold_of_r で相関係数の絶対値のしきい値を決めることができます。最終的に、x_selected という変数に、残った説明変数のデータセットが格納されます。
相関係数の絶対値に基づいて説明変数をクラスタリングするプログラムは demo_of_clustering_based_on_correlation_coefficients.py です。クラスターの数を決めるため、threshold_of_r で相関係数の絶対値のしきい値を決める必要があります。最終的に、x_selected という変数に、各クラスターから適当に 1 つの変数を選択したあとのデータセットが、x_averaged という変数に、クラスターごとに変数を標準化してから平均値を計算 (1 つのクラスターに 1 つの変数しかないときは、そのまなの変数) したデータセットが格納されます。
よろしければご利用ください。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


