わたしもついに Beware of … 系の論文を書いてしまいました。その名の通り、注意喚起する系の論文です。過去には他にこんなものがありました。
- Beware of q2!
- Beware of R2: Simple, Unambiguous Assessment of the Prediction Accuracy of QSAR and QSPR Models
- Beware of Unreliable Q2! A Comparative Study of Regression Metrics for Predictivity Assessment of QSAR Models
- Beware of ligand efficiency (LE): understanding LE data in modeling structure-activity and structure-economy relationships
- Beware of Naïve q2, use True q2: Some Comments on QSAR Model Building and Cross Validation
- Beware of External Validation! – A Comparative Study of Several Validation Techniques used in QSAR Modelling
今回は、r2 based on the latest measured y-values (r2LM) という、ソフトセンサー解析などの時系列データ解析のための新しい r2 を開発し、いろいろなソフトセンサー解析を行った論文が、Journal of Chemometrics に掲載されましたのでご紹介致します。
金子研オンラインサロン内ではこの論文を共有しています。ちなみに提案手法を実行できるコードはこちらにあります。
どうして時系列データで一般的な r2 を使うとダメなのか?
それは、実際にはモデルの推定性能は高くないにもかかわらず、テストデータを用いたときでも r2 が大きく(ときには 0.999 にも!?) なってしまうことがあるためです。なぜそうなるかについて説明します。
そもそも r2 とは、トレーニングデータを使った場合でもテストデータを使った場合でも、そのデータにおける目的変数 y のばらつきの中で、回帰モデル (たとえばソフトセンサー) によって説明できた割合をあらわす指標のことです。

テストデータの r2 は、r2T (r2 for test data) とか r2P (r2 in prediction) とか書かれることもありますね。たとえば r2T = 0.9 のとき、モデルはテストデータの y のばらつきのうち 90% を説明できた、と考えます。
r2 を式で表すとこちらにようになります。
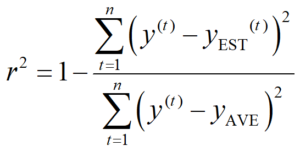
n がサンプル数、y(t) が t 番目のサンプルにおける y の実測値、yEST(t) が t 番目のサンプルにおける y のモデルによる推定値、yAVE が y の実測値の平均値です。分母が y の平均からの実測値のばらつき、分子が y の推定誤差のばらつきを表します。
時系列データのとき、t は時間的な意味合いを持ちます。t が大きくなるということは、それだけ時間が進むということです。
時系列データの特徴はいくつもありますが、r2 に関連するものは次の2つです。
- 時間的に近いサンプルの値が似ている
- トレーニングデータが更新される
1. について、横軸を時間にしたデータ点のプロットは、スペクトルデータに似ています。そのため、スペクトルデータの前処理と同じような処理が、時系列データにも使えたわけです。

2. についてはこちらに書いたとおりです。
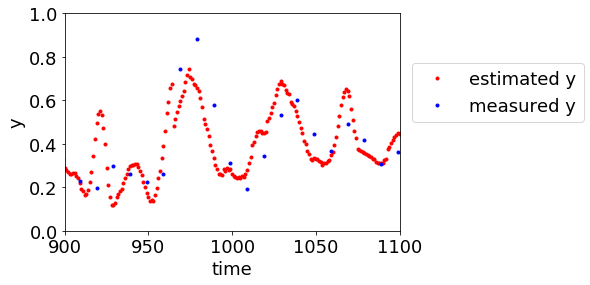
y の新しい測定データを使って、回帰モデル (ソフトセンサー) を再構築したり、次の y の値を推定できたりするわけです。
これらの特徴から、ある時刻の y の値を推定するとき、直近の y の実測値をその推定値として用いても、ある程度近い値になることが想像できると思います。回帰モデルがなくても、最新の y の実測値を、y の推定値として出力し続けていれば、そこそこ合ってしまうわけです。
このため、どんなモデルを用いたとしても、そしてテストデータで検証したとしても、r2 の値は大きくなる傾向があります。しかし、本来知りたいのは、回帰モデルによって、どれくらい y の値を説明できたか、です。時系列データを用いたときの r2 は、その知りたいことからかけ離れています。たとえば r2T = 0.9 のときでも、モデルによってテストデータの y のばらつきのうち 90% を説明できた、とはいえないわけです。
ではどうするか? → 直近の y からのばらつきを考えよう!
そこで r2 based on the latest measured y-values (r2LM) の登場です。式で表すと次のようになります。
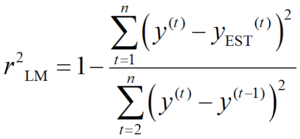
もともとの r2 と似ていますね。違うのは、yAVE → y(t-1) だけです。どういうことかというと、r2 では分母が y の平均値からのばらつきであったのに対し、r2LM は y の一時刻前の値からのばらつきなのです。こうすることで、時系列データのように、(値が似ている) 時間的に近い値があるなかで、回帰モデルによってどれだけ y を説明できたか、指標として表せるわけです。たとえば、テストデータにおける r2LM = 0.9 のとき、モデルによってテストデータの y のばらつきのうち 90% を説明できた、といえます。
論文ではいくつかのケースにおいてソフトセンサー解析を行い、r2LM の有用性を検証しています。
興味のある方は、論文をご覧になっていただけると幸いです。金子研オンラインサロン内ではこの論文を共有しています。またこちらの DCEKit で、便利に r2LM をご利用いただけます。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


