金子研の論文が ACS Omega に掲載されましたので、ご紹介します。タイトルは
Interpretation of machine learning models for datasets with many features using feature importance
です。
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
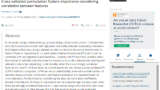
物性や活性が発現するメカニズムを解明するため、構築された回帰モデルを解釈し、y と x の間の関係を明らかにすることも重要です。LIME や SHAP では、あるサンプル点におけるモデルの形状の近似式を求めることで、そのサンプル点回りにおける y に対する x の影響の大きさを求めようとします。LOMP は、モデルを用いたシミュレーションに基づいて局所的に y に対する x の寄与を計算します。
LOMPにより、y に対する局所的な x の寄与もしくは方向性を議論するために使用できます。例えば y が最大値を持つサンプルに対して、さらに値を向上させる x の方向を議論できます。一方で、この論文ではデータセット全体における x の Globalな重要度について着目します。
例えば、ランダムフォレストをはじめとするアンサンブル学習法により x の重要度を計算できますし、Permutation Feature Importance (PFI) であればランダムフォレストに限らず様々な回帰分析手法と一緒に汎用的に使用できます。しかし PFI を計算するためには、トレーニングデータだけでなくバリデーションデータが必要であり、サンプル数が小さいときに重要度の計算が不安定になってしまいます。さらに、相関の強い特徴量間の PFI が、他の特徴量の PFI と比較して低く見積もられてしまいます。
そこで、Cross-Validated Permutation Feature Importance (CVPFI) が開発されました。
CVPFI ではモデル構築と特徴量の評価をクロスバリデーションに基づいて繰り返し行うため、従来の PFI と比較して安定して適切な x の重要度を計算できます。さらに x の相関関係に基づいて、他の特徴量の値もシャッフルするため、強い相関関係がある x でも独立した x と同様に、適切に x の重要度を評価できます。
CVPFI により x の相関関係を考慮した上で安定的に x の重要度を計算できるようになりましたが、特徴量が多いとき、それに応じて重要度の値も多くなり、x と y の関係や y の発現メカニズムを検討することが困難になります。x の相関関係を考慮することで、多くの特徴量で有意な重要度の値が割り振られ、それ自体は妥当なことですが、モデルの解釈はしにくいです。
そこで本研究では、x が多い場合に、x の重要度を用いてモデルを解釈する方法を提案しました。まず、そもそも特徴量が重要性は以下の三つで決まると考えます。
- y を説明する情報をもつ
- 他の特徴量で表現できない
- 他の特徴量を説明する情報をもつ
そこで CVPFI と x 間の類似度を用いてモデルの解釈について議論します。CVPFI が高く、互いに類似している x は、同様にモデルの解釈ができます。また、CVPFI がある程度しか大きくなくても、類似した x がない場合は、y に対して不可欠な情報を持つと考えられます。x 間の類似度の例としては、相関係数の絶対値や Maximal Information Coefficient (MIC) が挙げられます。
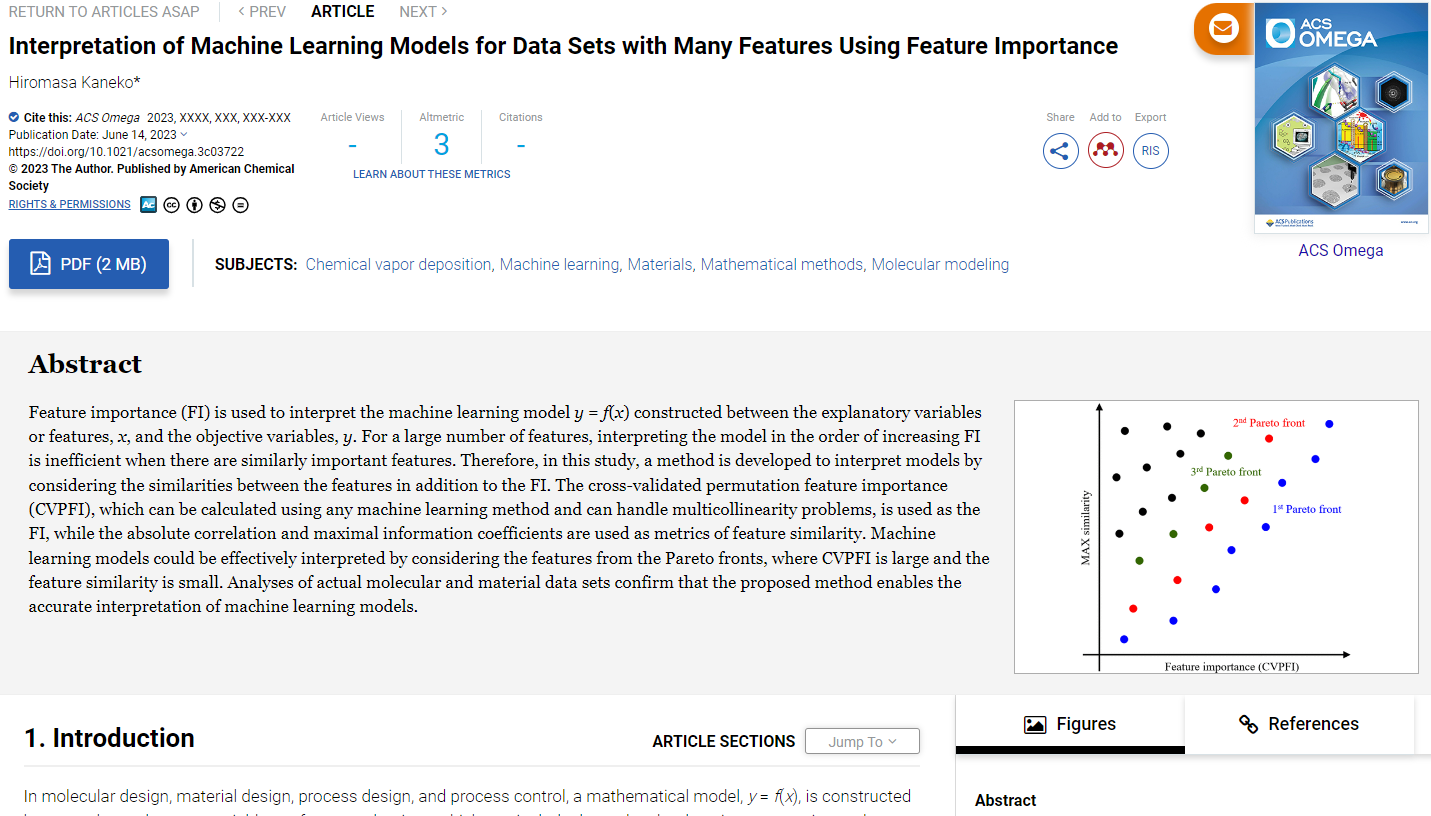
x ごとに、他のすべての x 間で類似度を計算し、その最大値を MAX similarity とします。MAX similarity が大きいほど、類似した特徴量が他に存在することを意味し、まとめて解釈することが望ましいといえます。横軸を CVPFI、縦軸を MAX similarity として特徴量をプロットしたとき、CVPFI が大きく MAX similarity が小さい領域、すなわち右下の領域に位置する x から解釈することが効果的です。ただし、CVPFI が 0 以下の x、すなわち重要でない x を解釈する意味はありません。そのため、CVPFI が正規分布に従うことを仮定し、CVPFI の平均値と分散から計算される正規分布の 0 以上の累積分布関数、すなわち CVPFI が 0 以上になる確率を計算し、それが閾値以上の x のみ解釈に用います。
初めに、CVPFI と MAX similarity の第一パレート最適解の x を抽出します。さらに、抽出された各x と類似度が高い x も同時に抽出します。具体的には類似度が閾値を超える特徴量を選択します。抽出された x を解釈した後に、次のパレート最適解 (第二パレート最適解) を求めます。ただし、既存のパレード最適解の x と類似した x は、パレート最適解には選ばれないようにします。以上の流れで、第三パレート最適解以降も抽出します。このようにして、解釈する x の順序を決め、類似した特徴量も考慮しながら、順番にモデルの解釈を検討します。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。