これまで、いろいろな企業やセミナーにおいて、ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクスの講義や、Python のハンズオンセミナーを行って参りまして、そのような経験・実績をふまえて、以下の動画を作成いたしました。すべて、動画中のパワーポイントのスライドを pdf 化したものが付いており、2. 以降は、jupyter notebook の (Pythonの) サンプルプログラムとサンプルデータセット付きです。
- ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクス全般 (1時間15分5秒)
- Jupyter Notebook の使い方・Python の基礎 (2時間30分8秒)
- データの前処理・データの可視化・回帰分析・クラス分類 (7時間5分21秒)
- モデルの適用範囲 (1時間21分4秒)
- 化学構造の扱い (59分25秒)
- 実験計画法・適応型実験計画法・ガウス過程回帰・ベイズ最適化 (3時間5分3秒)
背景、概要、質問したいときは?、内容、事前準備、利用条件・利用範囲の順に説明します。
背景
これまで、いろいろな企業の方や、セミナーを主催される方から、ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクスの講義や、Python のハンズオンセミナーを依頼され、お引き受けさせていただいてきました。月に 2 回のときもあれば、多きときは週に 1 回のペースのときもありました。たとえば Python のハンズオンセミナーはこんな感じです。

講義やセミナー自体は楽しいですし、データ解析・機械学習を化学・化学工学の分野でぜひ活用していただきたい、という強い気持ちももちろんあるのですが、他にもいろいろな仕事があるなかで

やはり、特に (共同研究を含む) 研究・教育の時間を確保したい、という思いから、最近はスケジュールを空けることを目指しています。

その取り組みの一環として、ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクスの講義や、Python のハンズオンセミナーについては、動画にしました。これまでの講義やセミナーの内容をベースにして、より丁寧に説明する資料・動画になっております。
概要
動画の概要は以下のとおりです (下にサンプル動画もあります)。
- ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクス全般 (1時間15分5秒)
- Jupyter Notebook の使い方・Python の基礎 (2時間30分8秒)
- データの前処理・データの可視化・回帰分析・クラス分類 (7時間5分21秒)
- モデルの適用範囲 (1時間21分4秒)
- 化学構造の扱い (59分25秒)
- 実験計画法・適応型実験計画法・ガウス過程回帰・ベイズ最適化 (3時間5分3秒)
それぞれに動画中のパワーポイントのスライドを pdf にしたファイルが付いてきます。そして 2. 以降は Jupyter Notebook のサンプルプログラムもあり、動画を見ながらそれを一緒に実行する形で、講義が進みます。
サンプル動画はこちらです。
このように、パソコンの画面とわたしの音声の動画になります。動画の形式・画質や音声の確認にご利用いただければと思います。また動画中のスライドの pdf ファイルはこちらです。
質問したいときは?
動画の内容に関する質問は、slack のチャットでお引き受けします。動画を購入されましたら、担当の方を動画専用の slack に招待します。そちらに質問を書き込んでいただければ、わたしがお答えいたします。特に質問の数に制限はありません。
内容
それぞれの動画の内容を説明します。
ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクス全般 (1時間15分5秒)
ケモインフォマティクス・マテリアルズインフォマティクス・プロセスインフォマティクスに関する基礎的なお話と、それぞれの研究内容のお話です。こちらは動画とスライドの pdf ファイルのみで、サンプルプログラムはありません。
内容については以下のスライドのタイトルをご覧ください。
スライドのタイトル
- データ・情報を活用した、いろいろな設計
- こんな化合物が欲しい!
- 構造活性(物性)相関
- シンプルな方法の例) 原子団寄与法
- 活性予測モデル構築手法 線形の一例
- 構造物性相関・構造活性相関
- 分子設計
- モデルは役に立っているのか?
- 分子設計:新しいポリマーを設計しよう!
- 分子設計:新しい医薬品を設計しよう!
- 分子設計:新しい記述子を開発しよう!
- 分子設計:配座異性体を考えよう!
- データ・情報を活用した、いろいろな設計
- 材料設計
- 適応的実験計画法
- どのように製造条件の候補を選ぶ?
- ケーススタディ①
- ケーススタディ②
- 材料設計:説明できる高精度モデルを作ろう!
- 材料設計: 結晶構造を考えて設計しよう!
- 分子設計・材料設計:高精度モデルを作ろう!
- データ・情報を活用した、いろいろな設計
- プロセス設計
- 効率的なプロセス設計 (適応的実験計画法)
- ケーススタディ
- プロセス設計:新しいプラントを設計しよう!
- データ・情報を活用した、いろいろな設計
- 化学工場(化学プラント)
- プロセス変数の時間プロットの一例
- ソフトセンサー
- ソフトセンサーの例
- ソフトセンサーを作成せよ!
- できました!
- ソフトセンサー例
- Process Analytical Technology (PAT)
- PATとは?
- Real Time Release Testing (RTRT)
- 制御設計:プラントの異常を診断しよう!
- 制御設計:膨大なプロセスデータを管理しよう!
- 制御設計:プラントのダイナミクスを考えよう!
- 問題点:ソフトセンサーモデルの劣化
- 適応型ソフトセンサー
- 制御設計: 適応型ソフトセンサーを設計します!
Jupyter Notebook の使い方・Python の基礎 (2時間30分8秒)
はじめに Python プログラミングをするためのツールである Jupyter Notebook の使い方を説明し、その後に、データ解析や機械学習を行うための Python プログラミングの基礎を説明します。NumPy, Pandas といったデータ解析や機械学習を行う上で重要なライブラリを使用したり、データセットの読み込みや保存を行ったり、データセットの特徴を把握するためのヒストグラム・散布図の作成、基礎統計量・相関係数の計算をしたりします。サンプルデータセットもあります。
データの前処理・データの可視化・回帰分析・クラス分類 (7時間5分21秒)
データセットを読み込んだ後に、データを前処理したり、主成分分析により可視化をしたり、目的変数と説明変数との間で回帰分析・クラス分類をしたりします。すべてサンプルプログラムが付いており、動画の中で一緒に実行しています。サンプルデータセットもあります。
説明およびサンプルプログラムのある回帰分析手法・クラス分類手法はそれぞれ以下のとおりです。
回帰分析手法
- 最小二乗法による線形重回帰分析
- 部分的最小二乗回帰 (Partial Least Squares Regression, PLS)
- リッジ回帰
- Least Absolute Shrinkage and Selection Operator (LASSO)
- Elastic net
- サポートベクター回帰 (Support Vector Regression、SVR)
- 決定木 (Decision Tree, DT)
- ランダムフォレスト (Random Forests, RF)
- アンサンブル学習
クラス分類手法
- 線形判別分析 (Linear Discriminant Analysis、LDA)
- サポートベクターマシン (Support Vector Machine、SVM)
- 決定木 (Decision Tree, DT)
- ランダムフォレスト (Random Forests, RF)
- アンサンブル学習
モデルの評価方法は、トレーニングデータとテストデータに分割して、トレーニングデータで構築されたモデルをテストデータで評価する方法ですが、最後にダブルクロスバリデーションも行っています。

さらに、モデルを構築したあとに新たなサンプル (目的変数が不明) に対する予測を行うの演習問題や、目的変数が複数の場合の回帰分析および新たなサンプルの予測に関する演習問題、そしてそれぞれの演習問題の模範解答のサンプルプログラムとその解説もあります。
内容に関しては以下のスライドのタイトルもご覧ください。
スライドのタイトル
- データセットの定義
- どうしてデータの前処理をするのか?
- オートスケーリング (標準化)
- オートスケーリングの例
- センタリング
- スケーリング
- モデル検証用(テスト)データのオートスケーリング
- データの可視化 主成分分析 Principal Component Analysis PCA
- 注意点
- 主成分分析 (PCA) とは?
- PCAの図解
- PCAで できること
- データセットの表し方
- PCAの前に
- 2変数のときのPCA (3変数以上への拡張も簡単)
- 主成分とローディング
- 行列で表すと・・・
- 第1主成分を考える
- ローディングの制約条件
- 主成分の分散を最大化
- Sを最大化するローディングを求める
- Lagrangeの未定乗数法
- Gを偏微分して 0
- 行列で表す
- 固有値問題へ
- 寄与率
- 累積寄与率
- 線形判別分析 Linear Discriminant Analysis LDA
- 線形判別分析 (LDA) とは?
- “最もよく判別する” とは?
- 重み w の求め方
- J の整理
- w を求める
- クラス分類の結果の評価
- クラス分類の結果の評価 例
- (参考) Kappa係数
- サポートベクターマシン Support Vector Machine SVM
- サポートベクターマシン (SVM) とは?
- 線形判別関数
- SVMの基本的な考え方
- サポートベクター
- マージンの最大化
- きれいに分離できないときは?
- 2つの項を一緒に最小化
- 重み w を求める
- 偏微分して0
- 二次計画問題
- 線形判別関数を求める
- 非線形SVMへの拡張
- カーネルトリック
- カーネル関数の例
- 最終的なSVMを作る前に最適化するパラメータ
- “良い”回帰モデル・クラス分類モデルとは何か?
- クロスバリデーション
- クロスバリデーションの補足
- グリッドサーチ+クロスバリデーション
- 最小二乗法による線形重回帰分析
- 回帰分析ってなに?
- 説明変数が2つのときの線形重回帰分析
- オートスケーリング(標準化)のメリット
- サンプルが n 個のとき
- 行列で表す
- 回帰係数を求めたい
- 最小二乗法
- 誤差の二乗和を回帰係数で偏微分して 0
- 回帰係数、ついに求まる
- 回帰モデルの精度の指標 r2
- 回帰モデルの精度の指標 RMSE
- 回帰モデルの精度の指標 MAE
- 部分的最小二乗回帰 (Partial Least Squares Regression, PLS)
- 部分的最小二乗回帰 (PLS) とは?
- どうして PLS を使うの?~多重共線性~
- 多重共線性への対策
- 主成分回帰 (PCR)
- PCR と PLS との違い
- PLS の概要
- PLSの基本式 (yは1変数)
- 1成分のPLSモデル
- t1の計算 yとの共分散の最大化
- t1の計算 Lagrangeの未定乗数法
- t1の計算 Gの最大化
- t1の計算 式変形
- t1の計算 w1の計算
- p1とq1の計算
- 2成分のPLSモデル
- w2、t2、p2、q2の計算
- 何成分まで用いるか?
- クロスバリデーション
- r2CV (予測的説明分散)
- 成分数の決め方
- リッジ回帰(Ridge Regression, RR) Least Absolute Shrinkage and Selection Operator (LASSO) Elastic Net (EN)
- RR・LASSO・EN とは?
- OLS・RR・LASSO・EN・SVR
- OLS・RR・LASSO・EN・SVRの共通点
- OLS・RR・LASSO・EN・SVRの違い
- 回帰係数の求め方
- どうしてLASSOは回帰係数が0になりやすいの?
- 重み λ, α の決め方
- サポートベクター回帰 Support Vector Regression SVR
- サポートベクター回帰 (SVR) とは?
- 基本的にSVRは線形の回帰分析手法
- 回帰係数 b
- 非線形の回帰モデルへ
- SVMとSVRとの比較
- SVRの誤差関数
- スラック変数
- RR・LASSO・EN との関係
- Lagrangeの未定乗数法
- 偏微分して0
- G の変形
- カーネル関数の例
- α を求める
- 二次計画問題
- SVRの回帰式
- サポートベクターとは
- c の計算
- SVRのまとめ・特徴
- C, ε, γ の決め方
- 決定木 Decision Tree DT
- 決定木 (Decision Tree, DT) とは?
- 決定木でできることのイメージ (回帰分析)
- 決定木のでできることのイメージ (クラス分類)
- 決定木モデルの木構造 (回帰分析)
- 決定木モデルの木構造 (クラス分類)
- 決定木のアルゴリズム
- 回帰分析における評価関数 E
- クラス分類における評価関数 E
- いつ木の成長を止めるか?
- ランダムフォレスト Random Forest RF
- Random Forest (RF) とは?
- RFの概略図
- どのようにサブデータセットを作るか?
- サブデータセットの数・説明変数の数はどうする?
- どのように推定結果を統合するか?
- 説明変数 (記述子) の重要度
- Out-Of-Bag (OOB)
- OOBを用いた説明変数 (記述子) の重要度
- 集団学習 (アンサンブル学習)
- アンサンブル学習の概要
- アンサンブル学習の概要
- バギング (Bagging)
- リサンプリング (resampling)
- サブモデルの統合
- アンサンブル学習のメリット・デメリット
- ダブルクロスバリデーション
- [参考資料]・プログラミング力向上のために・モデルの性能の指標 まとめ・トレーニングデータとテストデータの分け方・Y-randomization・説明変数の削減・Adaptive boosting (Adaboost)・勾配ブースティング
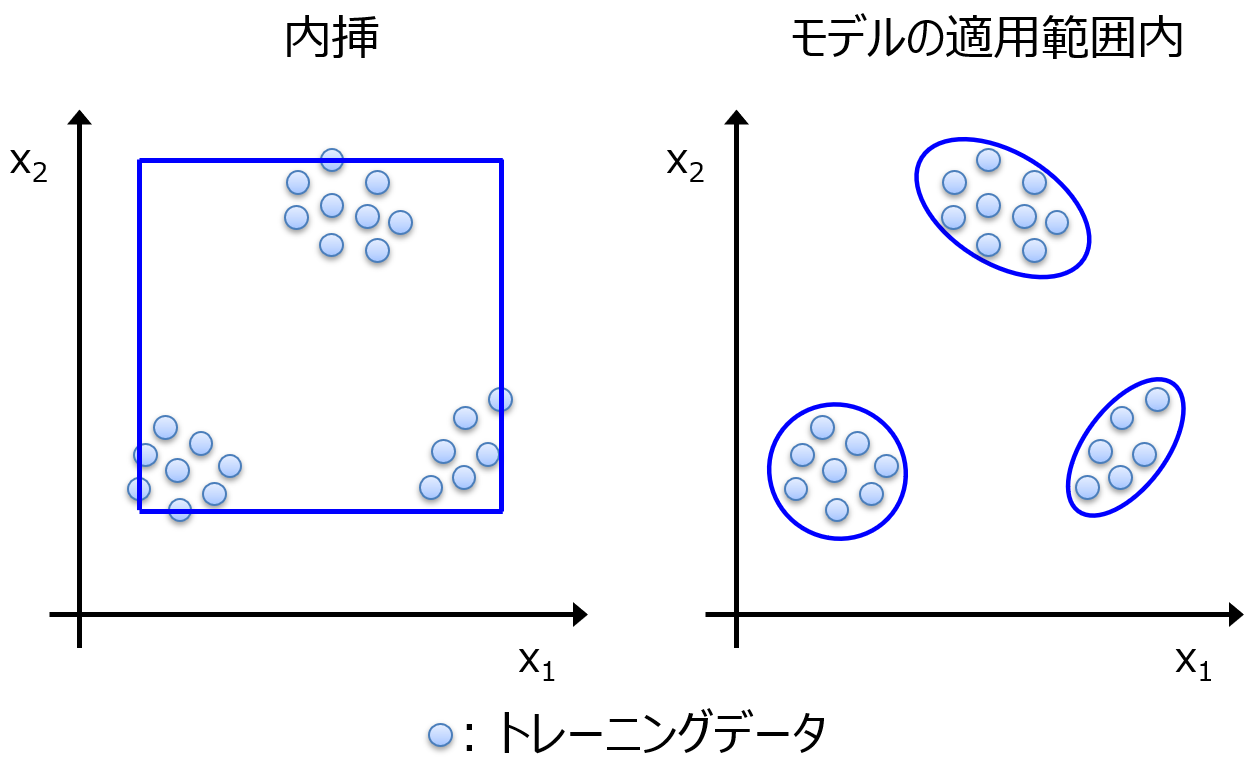
モデルの適用範囲 (1時間21分4秒)
回帰モデルやクラス分類モデルの適用範囲 (Applicability Domain, AD) についてです。

モデルの適用範囲を設定する方法を説明したり、サンプルプログラムではデータ密度とアンサンブル学習により実際にモデルの適用範囲を設定します。サンプルデータセットもあります。
内容に関しては以下のスライドのタイトルもご覧ください。
スライドのタイトル
- 一般的な回帰分析・クラス分類の基本的な流れ
- どんなXの値でもモデルに入力してよいのか?
- モデルの適用範囲・適用領域のイメージ
- モデルの適用範囲・適用領域
- AD の設定
- トレーニングデータの範囲
- トレーニングデータの中心からの距離
- データ密度
- データ密度
- k-NN法
- アンサンブル学習
- モデルとの距離 (Distance to Model)
- 回帰モデルの予測誤差(信頼性)の推定
- ケーススタディ: QSPR
- 回帰モデルの構築および検証結果
- DMと予測誤差の関係(バリデーションデータ)
- DMと予測誤差の標準偏差の関係
- テストデータの推定結果
- 注意!
- 数値シミュレーションデータで確認
- すべてのサブモデルで分類結果が一致した領域
- データ密度も使いましょう!
- ケーススタディ:QSPR
- 回帰分析
- 回帰分析 予測値の信頼性
- クラス分類
- クラス分類結果 k-NN
化学構造の扱い (59分25秒)
データ解析や機械学習を行うためには、データセットが数値化されている必要があります。化学構造を数値化することを目標として、化学構造の表現形式を説明したり、たくさんの化合物 (物性や活性あり) を扱うときのデータセットのまとめ方や扱う方法を解説したりしています。サンプルプログラムでは、実際に化合物のデータセットを読み込んで、物性・活性情報と化学構造情報に分け、化学構造情報に基づいて化学構造を数値化します。化合物のサンプルデータセットもあります。
内容に関しては以下のスライドのタイトルもご覧ください。
スライドのタイトル
- 化学構造の表現形式
- 分子を扱う一般的な流れ
- SMILES 形式
- MOL file 形式
- MOL file 形式
- たくさんの分子、そしてその活性・物性も!
- 構造記述子: 化学構造の数値化
- [補足] 2つの分子はどれくらい似ているか?
- [補足] 分子間の類似度の計算手順
実験計画法・適応型実験計画法・ガウス過程回帰・ベイズ最適化 (3時間5分3秒)
生成するサンプルの数を指定して、仮想的な説明変数 X の候補を生成したり、そこから実験計画法で少数のサンプルを選択したり、それらの目的変数 Y のデータが得られたとしてモデルを構築したり、モデルに基づいて次の X の候補を選択したりします。次の X の候補を選択する方法として、Y の推定値に基づく方法とベイズ最適化による方法があります。ベイズ最適化で必須なガウス過程回帰の説明もあります。
実験計画法・適応型実験計画法・ガウス過程回帰 (11 種類のカーネル関数)・ベイズ最適化それぞれのサンプルプログラムがあり、一緒に実行しながら説明しています。サンプルデータセットもあります。
内容に関しては以下のスライドのタイトルもご覧ください。
スライドのタイトル
- 実験回数を少なくしたい!
- 実験計画法
- 実験計画法のイメージ 1/3
- 実験計画法のイメージ 2/3
- 実験計画法のイメージ 3/3
- 実験パラメータの候補をどのように選択するか?
- D 最適基準が大きくなるように選択する
- [補足] D 最適基準以外の最適基準の例
- 最初に実験する候補を選択
- 標準化 (オートスケーリング)
- 次の実験候補を選択する
- 線形の回帰分析手法で対応できないときは?
- 簡単に非線形モデルを作る方法
- [参考] 非線形回帰分析手法
- [参考] 多重共線性の問題は?
- 例題をどうするか?
- ガウス過程による回帰 Gaussian Process Regression GPR
- ガウス過程による回帰 (GPR) とは?
- GPRの数値例
- GPRの数値例の結果
- GPRを理解するための大まかな流れ
- 説明に入る前に:GPRがとっつきにくい理由
- ① 線形モデルの仮定
- ① 簡単にするため、まずは X を1変数とする
- ② 回帰係数が正規分布に従うと仮定
- ② b の例
- ② サンプル間の y の関係を考える
- ② y の平均ベクトルと分散共分散行列
- ② 平均ベクトルと分散共分散行列の計算
- ② y の平均ベクトルと分散共分散行列 まとめ
- ② 何を意味するか?
- ② サンプルを生成してみる
- ② サンプリング
- ② サンプリングの結果
- ② 説明変数の数を複数に
- ② yの平均ベクトルと分散共分散行列の計算
- ② yの平均ベクトルと分散共分散行列 まとめ
- ③ 非線形モデルへの拡張
- ③ 非線形モデルへの拡張: カーネルトリック
- ③ カーネル関数の例
- ③ 非線形モデルのサンプリングの結果
- ④ y に測定誤差を仮定
- ④ yobsの平均ベクトル
- ④ yobsの分散共分散行列
- ④ yobsの分散共分散行列 まとめ
- ④ GPRのカーネル関数の特徴
- ④ GPRで使われるカーネル関数の例
- ⑤ 問題設定
- ⑤ 方針
- ⑤ 方針 まとめ
- ⑤ 用いる関係式
- ⑤ 同時分布 p( yobs,n+1 )
- ⑤ 条件付き分布 p( yobs(n+1) | yobs )
- GPRの使い方
- 精度 β
- GPRの数値例
- GPRの数値例の結果
- ハイパーパラメータの決め方 1/2
- ハイパーパラメータの決め方 2/2
- カーネル関数の決め方
- ベイズ最適化 Bayesian Optimization BO
- ベイズ最適化 (BO) とは?
- ベイズ最適化をするときの前提
- ガウス過程による回帰
- 回帰モデルを用いた探索
- 獲得関数
- Probability of Improvement (PI)
- PIの図解
- PIの式
- Expected Improvement (EI)
- Mutual Information (MI)
- 適応的実験計画法
- 注意
- [参考] 目的変数が複数の場合
- [参考] 一度に複数の実験候補を選択したい
- [参考] ベイズ最適化による化学構造生成
事前準備
動画のご購入を検討している方は、金子にご連絡ください。また検討している動画ごとに、事前に以下の確認をお願いします。
動画の 2. 以降では、Python を扱います。以下のページを参考にして、Anaconda をインストールして、jupyter notebook を起動できるかご確認ください。

また 「5. 化学構造の扱い」 を利用したい場合は、RDKit が必要です (この動画を購入しない場合は不要です)。以下のページを参考にして、RDKit をインストールしてください。

利用条件・利用範囲
社内であれば、個別に配布して構いませんが、社内での利用にとどめていただければと思います。想定している動画およびサンプルプログラムの使い方は、会議室・講義室などで動画を流して参加者が受講したり、個人に配布して個別に取り組んだり、といったものです。毎年お使いいただいても構いません (特に利用期限は設けておりません)。それ以外の使い方をしたい場合は、事前にご相談をお願いします。
二次利用は避けていただきますと幸いです。また動画の内容およびサンプルプログラムは、ぜひ研究・開発にご活用いただければと考えておりますが、ご自身の責任でご利用ください。
その他、ご質問・ご不明点などございましたら、遠慮なく金子までご連絡ください。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。