目的変数 Y と説明変数 X との間で、回帰分析やクラス分類を行い、モデル Y = f(X) を構築します。もちろん予測精度の高いモデルが望ましいですので、モデルの予測精度を上げるために、いろいろと工夫をします。その工夫の方針は、以下の 5 つです。
- Y を表現できる情報を X に追加する
- Y を表現する情報を X から抽出する
- Y と関係ない情報を X から除く
- Y と X が一貫した関係をもつデータセットにする
- モデルの適用範囲を広げる
そもそも X の中に Y に関連する情報がないと (極端な話、乱数の X しかないと)、どんな回帰分析手法、クラス分類手法を用いても、予測精度の良いモデルはできません。そこで、たとえば材料設計のときに Y が何らかの材料の物性であるとき、その物性と関連するような特徴量は何か、考えますし、プラントのプロセスデータを扱うときに Y が何らかの製品品質であるとき、その品質と関連するようなプロセス変数は何か考えます。ちなみに複数の物質が混ざっているときはこちらに書いたとおりです。

X の中に Y に関連する情報があっても、その情報を抽出してモデル化できないと意味がありません。X と Y の間の関係が非線形のときは、線形手法ではなく非線形手法を用いる必要があります。また関係が複雑で、さらにサンプルがたくさんあるときは、深層学習を用いるとよいです。ただ実際には、X と Y の関係がどのようなものかわかりませんので、いろいろな手法を検討することになります。

Y に関係する情報を X に含めることが大事な一方で、逆に関係しない情報が X の中にあると、モデル構築のときのノイズとなります。ノイズにもフィットするようにモデルが構築されてしまい、新しいデータ (モデル構築時のデータとはノイズが異なるデータ) に対する予測精度は下がってしまいます。いわゆるオーバーフィッティングです。Y に関係する X の情報がノイズに埋もれてしまい、適切に抽出できないこともあります。いわゆるアンダーフィッティングです。もちろん回帰分析手法やクラス分類手法で対処できる部分もありますが、事前にわかるときは、あらかじめノイズを除去しておくとよいです。

データセットの中に外れ値があったり、
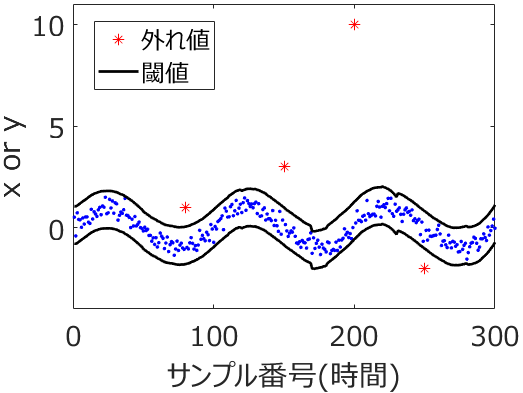
データセット内に X と Y の関係性が異なるサンプルが混在していたりすると、適切にモデル構築することができません。たとえば X と Y の間に直線関係があり、X と Y の直線がある傾きのサンプル群と、別の傾きのサンプル群とが一緒にあるデータセットでは、どのような傾きにしたらよいかわかりません。回帰分析手法やクラス分類手法を用いるときは、X と Y が一貫した関係をもつデータセットを使用しましょう。たとえば、Y とは別のカテゴリーの情報に基づいてサンプルを分割してからモデルを構築することが望ましいときもあります。
こちらに書いた通り、

モデルの予測精度は、いわゆる混同行列・正解率などや、実測値 vs. 推定値プロット・ r2 などだけでなく、モデルの適用範囲 (Applicability Domain, AD) の広さも関係しています。サンプルの数を増やしたり、X をうまく抽象化したりして AD を広げることを考えます。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。